Superconductivity and magnetic levitation

Parti 1

Hi, Billy!
Today we explore an exotic area of science, the Bermuda Triangle of Physics: superconductivity.
As soon as I mentioned superconductors, I am sure you thought about Carl Accounts or Jerry Overcooked, but even though I am sure Carl visited Bermuda very often and Jerry loves triangles, maybe with some pickles, this is not the case. I am talking about the phase transition that occurs when certain materials are cooled down below a characteristic critical temperature and an abrupt drop to zero electrical resistance and the expulsion of the magnetic flux density take place. I said superconductivity is an exotic phenomenon because these are its two main properties, but actually, they don’t happen whenever the conditions for superconductivity are satisfied. In fact, there exist different types of superconductivity, each of which is really peculiar. Moreover, this phenomenon is not fully understood yet and an air of mystery surrounds it; there are still details that need further investigation, especially as regards the so-called “High Temperature Superconductors”. Finally, superconductivity is extremely interesting also because it can be studied with different methods, that confirm already known results and give new information, for example the simple electromagnetic approach, the quantistic one, the Ginzburg-Landau theory and the Bardeen-Cooper-Schrieffer formulation. They are different not only in terms of analytical tools, but also they consider various points of view, someones macroscopical, some others microscopical.
An exhaustive explanation of superconductivity would require a quite difficult analytical approach, that exceeds our full comprehension. Since “little but good” is always our motto, Billy, we will rather choose a more qualitative profile, in order to understand its main physical concepts. Our final goal is to depict how two of the most exotic and surprising superconducting phenomena work: magnetic levitation and suspension. Despite the fact that superconductivity might appear as a purely abstract topic, actually some of its effects have a very practical use, for example magnetic levitation is responsible for the Japanese MAGLev trains.

Let’s now describe the main features of superconductivity.
As we already said, superconductivity is an intrinsic property of materials. Some examples of superconducting materials are pure elements like iron, aluminum, lead, mercury, but also some alloys, such as the cuprate YBa2Cu3O7 and Bi2Sr2Ca2Cu3O10. A superconductor does not always exhibit a superconducting behavior, but such a phenomenon manifests itself only under some specific conditions. Firstly, the temperature must be lower than a certain value, typical of each material. The problem is that usually this value is located in the cryogenic range. The critical temperature of the pure elements we mentioned before is about 10 K, which corresponds to -263 °C, quite distant from the temperature of your ordinary domestic freezer, Billy. The cuprate materials, on the contrary, are High Temperature Superconductors, whose critical temperature is about 100 K (-173 °C). This is still far below room temperature, but at the same time much easier to reproduce. In fact, a simple bath of liquid nitrogen ensures a temperature equal to 77 K, that thus enables the phase transition to superconductivity. Then, you can see, Billy, that working with superconductors requires a remarkable technological effort: sometimes, the energy required to guarantee superconductivity is much higher than the one actually generated exploiting its effects, so that costs become larger than advantages. Recent researches are then intended to find out new compositions that act like superconductors with a critical temperature as high as possible.
The other requirements that must be fulfilled in order to give rise to superconductivity concern the entity of the applied magnetic field and of the injected transport current, indispensable ingredients of the phenomenon. There exists a maximum limit for each of them, otherwise the existing conditions of the carriers responsible for superconductivity do not subsist anymore and the sample behaves like a normal conductor. The region in which superconductivity is allowed is represented in the figure below, in yellow.

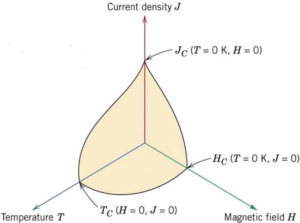
Indeed, the most important role in this phenomenon is played by some special carriers that we can call superelectrons. Superelectrons are Cooper pairs, that consist of a couple of normal electrons, bounded to each other thanks to some kind of energy. This is one of the highlights of the BCS theory, that we will not explore further. It is sufficient that only one parameter out of the 3 we mentioned above overcomes the corresponding threshold, so that the energy acting on the pairs (thermal or kinetic) is larger than the one that keeps the 2 electrons united and the couples split up. Here, the thermodynamic nature of the phenomenon emerges. The phase transition that takes place once the temperature is below Tc (critical temperature), then, is not abrupt and sudden, but quite gradual. As temperature decreases, more and more normal electrons combine, creating Cooper pairs. In other words, at T=Tc the formation of the first couple occurs and at T=0 K there are no single electrons: the transition to the superconducting state is complete.
Of course, Billy, only superelectrons are endowed with “superproperties”. These are a zero electrical resistance and the expulsion of the magnetic flux density.
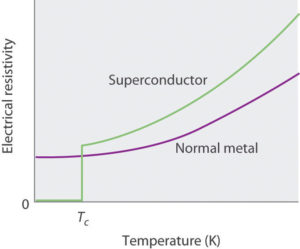
Let’s focus on the first peculiarity. The electrical resistance is a measure of the difficulty of an electric current to pass through a conductor. The higher the resistance, the larger the effort, the bigger the loss. In fact, the resistance subtracts useful energy, making the conductance less performant. This lost energy is converted into heat, according to the so called Joule effect. Sometimes, the Joule effect and the resulting heat is the real purpose of a device, like in a hair dryer or a toaster (for Jerry Overcooked’s happiness), but most of the times it is only a side effect that we aim at removing. In our case, we model the resistance on the base of the scattering mechanism, as collisions between electrons and ions that interrupt the continuous flow of current. However, if the frequency of the applied field is such that its period is much shorter than the time between two consecutive collisions, a superelectron rapidly changes its trajectory due to an inversion of the field polarization and the probability to collide against other particles gets smaller. Its mean free path (= the distance covered by the superelectron between two consecutive collisions) becomes ideally infinite and dissipation and resistance are ideally null. In reality, resistance is not perfectly trivial, there is always a little residual component of losses due not only to normal electrons that have not coupled into Cooper pairs yet, but also to the superelectrons themselves, that can be neglected, though. Billy, this characteristic represents a huge advantage in terms of quickness and efficiency. However, superconductors in a normal state have a resistance much higher than natural normal metals. This emphasizes the importance of the cooling system and the field source control, in addition to the composition of the material. Any defects could jeopardize the performance of the sample.

Let’s now pass to the second property. The expulsion of the magnetic flux density is known as Meissner effect. Don’t worry Billy, we will perform an experiment in order to clarify this concept. More specifically, we will compare the results of 2 experiments:

1. Zero Field Cooling: let’s consider a superconducting sphere. Firstly, we reduce the temperature below Tc, then we apply a magnetic field.
2. Field Cooling: the procedure is similar to the previous one, but the chronological order of the sequence is inverted. Firstly, we apply an external field and then we decrease the temperature.

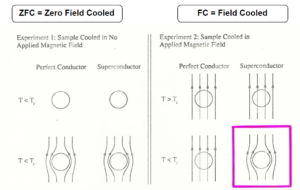
A perfect conductor is a non-superconducting normal material that in a proper spectral range exhibits the lossless condition. In the figure, the circle represents the sphere and the curves the field lines. We can observe that the ZFC operating mode returns exactly the same results both for the normal and the superconducting samples. On the contrary, the FC configuration gives two different outcomes: while the normal conductor admits a finite static magnetic flux inside it, the superconducting sphere repels the field lines. Nevertheless, the penetration of the magnetic field is not completely contrasted, the sphere allows it in a thin superficial layer. The field confined in this coat gives rise to supercurrents, that in turn generate a magnetic field opposite to the external one. The final result consists in a compensation of the two fields inside the sphere, that produces a null total field, ending with the Meissner effect.

Dear Billy, this is only a very general and first smattering of superconductivity. In the next episodes, we will survey the different kinds of superconductors with the corresponding peculiarities and finally the levitation and suspension phenomena, where the Meissner effect plays an essential role.

Part 2

A trace of wondering surrounding the discovery of superconductivity persists even today. Books about it begins like fairy tales: ”In Leiden in 1911, Kamerlingh Onnes…”. Only the “Once upon a time is missing”.

However, we are romantic spirits, Billy, so we can create a poetic and engaging framework to the infinite masterpiece of superconductivity. Then…

Once upon a time, Kamerlingh Onnes was studying the reduction of resistance at low temperatures in Leiden, focusing on mercury. The most challenging endeavour for him was how to reproduce a temperature near to absolute zero (-273 °C). Even in the most rigorous Siberian winter, temperature gets only very rarely below -60 °C. Leiden was the only place in the world at that time where anyone knew how to create such an intense cold. After a lot of attempts and disappointments, Onnes’s mission regarding the resistivity of solid mercury at cryogenic temperatures was finally accomplished by using liquid helium as a refrigerant. On April 8, 1911, 16:00 hours, Onnes noted "Kwik nagenoeg nul" on his notebook, which in elfin Dutch translates as "[Resistance of] mercury almost zero.". He observed that at the temperature of 4.19 K, resistivity abruptly disappeared, becoming thousands of times less in amount relative to the best conductor at ordinary temperature. Onnes later reversed the process and found that at 4.2 K resistance became again relevant in the material. The scientist, proud and excited, immediately understood the importance of his discovery and tested it performing an experiment. Onnes introduced an electric current into a superconductive ring and removed the battery that generated it. Upon measuring the electric current, Onnes found that its intensity did not diminish with time. The current persisted due to the superconductive state of the conductive medium, since no resistance was obstructing it. Eureka! Onnes published articles about the phenomenon and, for his research, he was awarded the Nobel Prize in Physics in 1913.

By 1913, physicists from all over the world were looking forward to making pilgrimages to Leiden to observe Onnes’s remarkable result. However, in 1914 other events were occurring in Europe that temporarily eclipsed the discovery of superconductivity. Although Holland remained neutral in the Great War, all researches at Leiden were forced to stop until 1919, when the Leiden group started to work on superconductivity again, discovering a number of new superconducting elements, for example tin.

Some years later, Leiden was not the reign of liquid-helium any longer because this special skill became available also in other countries. The German Walther Meissner rapidly became a Master of liquid-helium and in 1933 he started an experiment designed to determine whether the current in a superconductor flows on its surface or in its bulk. A very small coil was used to measure the magnetic field between two cylinders of tin, carrying current in parallel. Meissner chose his valiant pupil Robert Ochsenfeld to carry out the experiment. The result was dramatic and unexpected: even when the tin cylinders were not carrying any current, the magnetic field between them increased when they were cooled into their superconducting state. Such an increase just outside the sample was due to an expulsion of the applied field inside the material, resulting in a denser and not uniform distribution of the field lines in the immediate external region. This was a piece of evidence that superconductors were not only perfect conductors (zero resistance), but also perfect diamagnets (repulsion of magnetic flux density). This latest discovery was curious, but nobody could understand its real and huge potential in practical use, yet: magnetic levitation. However, the discovery of the Meissner effect was a crucial turning point: superconductivity acquired the status of thermodynamic phase transition.
In 1934, a couple of German brothers, Heinz and Fritz London, were studying the electromagnetic behaviour of superconductors, in Oxford. They had fled from Germany because of the Nazis’ race laws, looking for a more peaceful and safer atmosphere. So far, superconductivity had introduced new experimental knowledge, that seemed to clash with the ancient Sacred Commandments of Physics: Maxwell’s laws. Thus, they work hard to adapt Maxwell’s laws on the base of the two main properties of superconductors, in the light of the principle of coherence and symmetry that governs the world. They ended up with the so called London equations, where an important role is played by the “London penetration depth”, which defines the thickness of the superficial layer in which supercurrents arise, guaranteeing that Meissner effect takes place.

The Second World War interrupted research in superconductivity just as the First World War had done in the past. During these dark period, scientists’ attention was focused, by choice, by force or by misunderstanding, on other physical issues, whose purposes were not always so noble. Light shone again on superconductivity in the ‘50s, when real progress began once again to be made. This was a greatly fruitful decade: new important characters came out, whose contribution had been exceedingly precious, not only for the new results themselves, but also because the interconnections between the different perspectives became clearer and clearer.

At the beginning, the phenomenon still resisted any true microscopic understanding, but some pieces of the puzzle did begin to come together, particularly in the phenomenological model of Vitaly Ginzburg and Lev Landau. The Ginzburg-Landau theory managed to combine important elements of the Londons’ picture of superconducting electrodynamics with Landau’s earlier analysis of second-order phase transitions, based on symmetry observations. In the meantime, a young theorist in Landau’s group in Moscow, Alexei Abrikosov, proposed a new class of superconducting materials, that he then called “Type II superconductors”. One day, during his researches, he discovered that not all superconductors are characterized by a critical surface that clearly separates the normal behaviour by the superconducting state, where Meissner effect occurs. Some of them exhibit a particular third intermediate state which admits the penetration of flux lines, not continuously, but in a regular arrangement of discrete entities: the future Abrikosov vortex lattice. Scientists will soon understand that the interaction of such a peculiarity with the Meissner effect is able to produce the result we are looking for.

Another team was about to take part to the endeavour: John Bardeen, already well-known for his work leading to the discovery of the transistor, Leon Cooper and John Robert Schrieffer. Bardeen had to leave them for some months in 1956, when he had to go to Stockholm to be awarded the Nobel Prize for the transistor, but he joined again his two companions in 1957. They focused on the microscopic aspect of superconductivity and worked furiously, because they were afraid to be scooped by Richard Feynman. In fact, he was a fearsome rival since he was working on the same topic; the hints he caught and his intuition were rapidly bringing him near the solution, becoming a threat for the coveted award: prestige, glory, and, why not, the Nobel Prize.
However, finally it was not Feynman, but Bardeen, Cooper, and Schrieffer who produced the microscopic theory: an elegant formulation which takes into account all of the puzzling phenomena of superconductivity and succeeds in making new predictions, shortly after confirmed by experiment. They won the Nobel Prize in 1972 (the second for Bardeen) for what will soon become popular as the BCS theory.

Almost 50 years after its discovery, superconductivity could, at long last, reasonably be said to have been explained, at least in its main aspects.

And everyone lived happily ever after…

Part 3

 

Welcome back Billy! Have you fallen asleep serenely after the bedtime story of the last time? I hope so, also because you now need to be full of energy and enthusiasm to face the continuation of our travel through the mysteries and the secrets of superconductivity. The exploration is becoming tougher and tougher, in fact, we need to introduce some more technicalities, but always within a qualitative framework. You already had some hints about the evolution of our dissertation by reading the story. Some names and discoveries were already known, while you heard some others for the first time. Today, we will deepen our knowledge about type II superconductors, that, as you can remember, were introduced for the first time by Alexei Abrikosov. In particular, we will focus on their interaction with the Meissner effect, so that we are closer and closer to our final goal: a true understanding of magnetic levitation and its free-suspension counterpart.

As we already told, any sufficiently big superconductor immersed in a small enough magnetic field will create non-dissipative supercurrents confined in a thin skin on its surface. They induce a magnetic field that counterbalances and cancels out the externally applied field in the material. Therefore, a superconducting sample can expel the external magnetic field to produce a null magnetic flux density in its interior (perfect diamagnetism), provided that the field is kept in a specific range of strength. This behaviour is known as the Meissner effect.
After the bedtime story, Billy, we are now aware that there exist two kinds of superconductors: type I superconductors, endowed with a normal and a superconducting state, and type II superconductors, which comprehend a third intermediate phase, called vortex state. Most pure elements are type I superconductors, while most alloys and all HTS belong to the type II family.
So far, we have always referred to type I superconductors, that exhibit Meissner effect up to a thermodynamic critical field Hc, at which superconductivity is destroyed and the field fully penetrates into the sample. Above this value, the material is in the normal state.
On the contrary, type II superconductors are characterized by two critical surfaces, that share the same critical temperature, but have two different critical fields and critical current densities. In this case, the Meissner effect is only observed for magnetic fields below a lower critical field Hc1 and superconductivity is destroyed for fields above an upper critical field Hc2 (Hc1 < Hc2). For magnetic fields between these two values, the material is not perfectly diamagnetic and it is said to be in a mixed or vortex state. Indeed, the field is allowed to enter the material, not uniformly, but in discrete arrays of entities known as vortices.

Vortices represent the most peculiar objects in superconductivity. The vortex state is denoted also as mixed state because this third intermediate phase consists of the coexistence of both normal and superconducting state. In fact, we can figure out vortices as cylinders made of normal material, immersed in a superconducting ambient, usually displayed in a hexagonal arrangement, known as Abrikosov vortex lattice. In other words, they are normal cores cylinders surrounded by circulating supercurrents. The crossing of Hc1 determines the entrance of the first vortex in the sample, from its sides. The larger the applied magnetic field (still below Hc2), the more vortices enter the material, the more densely packed they are. As mentioned above, they tend to acquire a hexagonal arrangement, so that their reciprocal distance is maximized, due to the repulsive interactions among them.

Then, at the upper threshold between mixed and normal state, vortices are so near to each other that the superconducting space that separates them can be neglected, and the sample is entirely normal. Vortices are discrete entities as a consequence of the fluxoid quantization, but, my dear Billy, this is another story. The most important aspect for us is that they are made of normal material, that means that they are not subject to the two main properties of superconductors: they are provided with a certain resistance and they do allow the penetration of an applied field.

Now, Billy, it’s time to go a step further. Type II superconductors admit two subclasses: reversible and irreversible superconductors.
Reversible superconductors are flawless, homogeneous samples where vortices feel the influence of two competitive forces: the Lorentz-like force and the drag one. The former is due to the fact that an external magnetic field is applied to the material and it tries to remove vortices out of the superconductor, pushing them back towards its sides. The latter derives from the normal nature of vortices. It is possible to prove that for a constant driving current and constant applied field, dissipation is constant and vortices move across the sample at constant speed. Consequently, in light of the first principle of dynamics, in addition to Lorentz-like force, there must be also some other drag force opposing the flow of vortices, that is the cause of power dissipation. Such drag force is a manifestation of resistance. This means that a reversible type II superconductor is globally devoid of the first property typical of superconductors and they behave like normal conductors. Thus, we can say Billy that reversible superconductors are useless.
Now, Billy, you will say: “So much effort for nothing! Everything has been worthless!”, but don’t be demoralized, the best is yet to come. Our secret weapon are irreversible superconductors.
Irreversible superconductors are inhomogeneous materials, that consist of type II superconductors provided with defects, for instance impurities, vacancies and dislocations. Such defects act like pinning centres, that are the origin of irreversibility, indeed. In fact, depending on the entity of the applied field and of the current density, they represent energetically favourable sites for vortices: as soon as a vortex enters the material and meets a pinning centre, it gets trapped in its position. Therefore, every vortex feels the influence of two opposing forces, once again: one is the Lorentz-like force we mentioned before, that tries to remove vortices, the other is the pinning force, that keeps them blocked in a certain place. It is possible to show that power dissipation (then resistance) is mainly due to the movements of vortices. Then, as long as vortices remain fixed, resistance is negligible. We have finally depicted the material we will use for our experiment: magnetic levitation.

We can conclude that pinning is intimately connected to the superconducting behaviour of a material. Dissipation, thus the transition from superconducting to normal state, arises whenever either of these two events takes place: depinning, when a vortex is separated from the defect and becomes able to move, or depairing, when the Cooper pair that constitutes the superelectron breaks, generating two single normal electrons.
Now, only the last piece of the puzzle is missing: the hysteretical behaviour of magnetization in a superconductor. Don’t worry Billy, no one is getting crazy! We have presented all the ingredients we need to finally describe and understand magnetic levitation. We will see how an irreversible type II superconductor, vortices and the Meissner effect interact in order to reproduce one of the most enchanting physical phenomena.

Part 4

THE MEISSNER EFFECT DOESN’T TAKE PLACE IN IRREVERSIBLE TYPE II SUPERCONDUCTORS.

Oh, now I feel better. This article starts off with a bang, doesn’t it, Billy?

Oh, Billy, I couldn’t keep the secret any longer, it took a lot of effort to me so far. But I am sure you are the rip-the-plaster-off sort of person. Now, if this surprising piece of news hasn’t knocked you out, I will justify my affirmation. This is the last chapter but one of our dissertation about superconductivity and there is still so much to do. Then, sleeves up… and working!

Let’s consider, Billy, a parallelepiped of irreversible type II superconducting material, infinitely extended into two dimensions, so that only one gives non-trivial results. This is the simplest case, which enables us to better understand the concept. Let’s focus on this transversely finite-sized face and apply a magnetic field parallel to its longitudinal direction, increasing its magnitude progressively. Once the amplitude of the magnetic field has overcome the threshold Hc1, the first vortex enters the material. However, the sample is provided with plenty of defects, that act like energetically favourable sites. Therefore, as soon as the vortex meets a pinning centre, it gets blocked in its specific position. This occurs for each incoming vortex, so that in short time, the slab presents a really inhomogeneous distribution of vortices, since they are concentrated mainly near the two sides and no vortex is located in the central part.

As the external field grows further, the Lorentz-like force might become larger than the pinning one, then a vortex gets discarded from the corresponding pinning centre and starts to wander again, in search for the next nearest defect. This is likely situated in a more internal region of the slab, since all the other pinning centres are already occupied. At the same time, since vortices move always from the side to the centre and the more external pinning centres are already engaged, the outer vortices constitute a thin peripheral barrier, that hinders the access of new vortices and attempt to prevent any further “intrusion”. We can say, Billy, that the slab tends to counteract flux penetration through a shielding reaction. Thus, while the applied field is larger and larger, additional vortices penetrate into the sample, always starting from the sides and eventually migrating towards the centre, defect by defect, but at increasing difficulty. Finally, the material will exhibit a strongly non-uniform vortex distribution, much denser on the sides rather than in the central part.

This is the result of the material repulsive behaviour, that we can define as a diamagnetic response. In other words, the sample tries to prevent as much as possible the penetration of the applied field, represented here by the normal core vortices, attempting to reproduce the Meissner effect, but without completely succeeding in it.
However, Billy, pay attention: we are still studying the mixed state, not the superconducting one, where Meissner effect actually takes place, so we have not justified the opening sentence yet.

So far, we have studied the behaviour of the slab when the applied field gets gradually increased. Now, beginning from the strongly inhomogeneous vortex distribution we have just realized, let’s perform the opposite operation: let’s reduce the external field. Please Billy, notice that we are proceeding with the same sample of before, extending the experimental sequence.
Here, the coup de theatre.
When the applied field gets decreased, the flux distribution can’t be described simply by reversing the previous behaviour. For certain, a reduction of the applied field determines a reduction in the number of vortices, since they are the carriers of the magnetic flux density. However, as the penetration of vortices was contrasted when the field was increasing, once the vortices have settled in the material, on the contrary, the sample tries in every way to retain the vortices inside itself. It struggles to avoid that vortices run away, in order to maintain the previous level of magnetization as much as possible.

It exerts such an intense attractive force on the vortices, that even when the applied field has been reduced so much that it has vanished, there are still some vortices in the superconductor.

But, hey hey Billy, what is happening? Vortices with no applied field? If the applied field is null, it means that its value is certainly below Hc1, then we are in the superconducting state! But how can vortices survive if we are in the superconducting state? What about the Meissner effect and the expulsion of the magnetic flux density? Have I made fun of you so far? Eh eh Billy, that’s just it, old sport! The Meissner effect doesn’t take place in irreversible type II superconductors. And we have finally justified the very first sentence.
This fact has enormous consequences, both from the theoretical and the practical point of view. Firstly, such a result implies that the Meissner effect is not the best proof for showing superconductivity any longer. Moreover, this is possible if and only if we realize a procedure similar to the one we have performed. This means that the chronological order of the experiment is extremely important and the magnetization of the superconductor depends on its history, that in technical jargon we call a “hysteretical behaviour”.

In addition, the fact that the sample is provided with vortices, then with a certain residual magnetic force, even when the applied field is absent, indicates that we have turned the superconductor into a… magnet! But not an ordinary magnet, Billy… a supermagnet! A supermagnet is 10 times stronger than the magnets you have on your whiteboard at home! Imagine the Geomag structures you could build up with supermagnets! However, there is always this tiny little detail: you need a refrigerant system that is able to cool down temperature below at least 77 K…

Part 5

 We are finally about to reach our goal, Billy. The wait is over. This is the last chapter of our long, strenuous, yet satisfying exploration of the phenomenon of superconductivity.

Like any self-respecting season finale, this article deserves its own  “Previously on… Superconductivity and magnetic levitation”:

• Chapter 1: we introduced superconductivity as a phase transition that takes place at a specific critical temperature, typically in the cryogenic range, and requires some applied field and current density requirements to be fulfilled. Its main properties are null resistance and the Meissner effect. Moreover, we emphasized the fact that superconductivity can be described from different points of view, but it is still far from full comprehension.
• Chapter 2: we briefly summarized the most important moments in superconductivity’s history; in particular, we have mentioned Onnes (discovery), Meissner, the London brothers (electromagnetic approach), Ginzburg and Landau (II order phase transition), Abrikosov (vortices) and finally Feynman, Bardeen, Cooper, and Schrieffer (microscopic theory).
• Chapter 3: we said that there exist 2 kinds of superconductors: I type and II type superconductors, that are provided with an additional third intermediate state, the vortex state. The latter envisions 2 possible varieties as well, reversible and irreversible superconductors. Vortices play a fundamental role in irreversible superconductors, which are the material we are interested in for magnetic levitation.
• Chapter 4: we focused on irreversible II type superconductors and depicted their peculiar hysteretical behaviour, resulting from the interaction of vortices with pinning centres (defects of the material able to block vortices since they represent energetically favourable sites).

My dear Billy, this was a demanding, but necessary premise to eventually get into the core of our dissertation: magnetic levitation and its counterpart, magnetic suspension. Here we are, at last. I am sure, Billy, that you are a big fan of “Fisici Senza Palestra” and that you have loyally and accurately read all our articles, Monday by Monday. Then, now I suppose you are sufficiently prepared to engage to a pure and formal physical experiment. I can feel your goose bumps, both of pleasure and concern.

Let’s begin first with magnetic levitation, which is performed in Zero Field Cooling operating mode.

As we already described in the first article, the ZFC technique consists in subjecting the superconducting sample to the effect of a magnet, after is has already been cooled down below its critical temperature. The sample we use is a textured Y Ba2Cu3O7 material, an irreversible II type superconductor whose critical temperature is Tc = 92 K. It undergoes the action of a Nd-Fe-B permanent magnet. Given Tc, liquid nitrogen is suitable as cooling bath, since its boiling point is attained at T = 77 K < Tc. The experimental setup of this experience follows:

As we approach the magnet to the superconductor once it has reached T = 77 K uniformly, it does not come into contact with the sample, but it levitates above it. The physical interpretation of such a behaviour is due to pinning. The displacement of the magnet modifies the distribution of the vortices, but the pinning force reacts trying to oppose to any variation. Vortices find difficulties in entering the material because of the pinning centers; therefore, the magnet is repelled by the superconductor. It levitates at a height given by Fp = Fg = mg, where the weight of the magnet is perfectly counterbalanced by the force exerted by the superconductor (equilibrium). When the magnet is perturbed by an external force, it responds like it was connected to the superconductor through a spring: restoring forces tend to bring the magnet back to its original position through oscillations, until it reaches equilibrium thanks to damping. Stiffness is another important parameter that characterizes any spring: it is a measure of the resistance to deformations, so, in this case, it is related to the stability of the levitation. We aim at obtaining the most stable possible interaction between the magnet and the superconductor, implying then the higher the stiffness, the smaller the oscillations, the better the stability. At the same time, damping introduces energy losses, so it might seem detrimental to the phenomenon. However, damping is essential for stability as well since it extinguishes oscillations, otherwise uncomfortable in practical applications, for example the Japanese MAGLev trains. No one wishes to travel on a bouncy train, do they Billy?

Magnetic suspension can be considered the dual of levitation. In fact, it must be accomplished in Field Cooling mode, which performs the inverse procedure with respect to ZFC: firstly, an external magnetic field is applied to the superconductor; then, the sample is cooled down below its critical temperature. The experimental setup follows:

 

Here, the geometry of the setup is also reversed. Since we are investigating suspension, now the superconductor must be located above the magnet with a proper support. Once liquid nitrogen has been poured in the container and the temperature of the sample has become 77 K, we can observe the desired phenomenon: the magnet floats in the air, correspondingly to the sample position. The cause of such a phenomenon is still pinning, yet with an opposite result. In the previous article we said that Meissner effect is not the best proof for showing superconductivity. In fact, this is a piece of evidence for it. In ZFC, the sample felt no magnetic field before the phase transition to the superconducting state, then no vortices were contemplated inside the sample, due to the pinning's repulsion effect. On the contrary, in FC the material is fully penetrated by a magnetic field before becoming effectively superconducting, then, as soon as T < Tc, the sample is inhabitated by plenty of vortices. The Lorentz-like force tries to expel them, but they are blocked inside the superconductor by the pinning centers. Some of them could survive also when H < Hc1, then Meissner effect does not take place. The tendency of the sample to retain vortices results in an attraction effect. This is the reason why the magnet is suspended in the air, provided that Fp ≥ F = mg.

Let’s celebrate Billy, we have crossed the finish line! I am proud of your commitment, effort and curiosity! I hope you have really appreciated our travel through the mysteries of superconductivity.

But don’t feel sated, new adventures are coming!