How cool is cooling? (o Il laser cooling)

Il laser cooling è un processo che consiste nel raffreddamento di un fascio di atomi per mezzo di laser che sfruttano l’allargamento della riga di assorbimento e l’effetto Doppler, per raggiungere temperature vicine allo zero assoluto.

Tutto chiaro Billy? Dalla tua faccia mi sembri perplesso. Forse è meglio procedere con ordine.

Immaginiamo di avere un gas perfetto, le cui particelle, come noto dalle teorie cinetiche, si spostano con una velocità quadratica media pari a 

$$v_{qm}=\sqrt{\frac{3k_{B}T}{m}}s=4$$

dove k_B è la costante di Boltzmann e m è la massa. Raffreddare un gas equivale dunque a diminuire vqm, cioè rallentare le sue particelle. Per fare questo, nell’ipotesi che si conservi la quantità di moto totale del sistema, risulta efficace sparare fotoni contro gli atomi che si muovono nel verso opposto, in modo da rallentarli. Come sorgente di fotoni scegliamo un laser, ovvero un dispositivo in grado di emettere un fascio di luce coerente, monocromatica e concentrata in un raggio rettilineo estremamente collimato attraverso il processo di emissione stimolata. In breve, si tratta di una luce le cui particelle sono perfettamente ordinate, come schiere di soldati identici in marcia con la stessa cadenza. La luce ordinaria invece è come la gente in un centro commerciale in periodo di saldi, che corre frenetica qua e là in preda a un raptus di follia alla ricerca dell’affare del millennio.

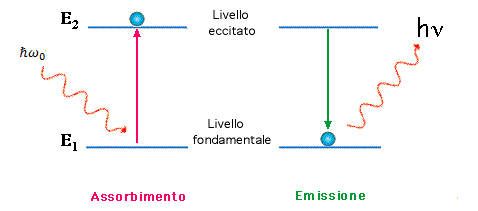
Affinché il fotone rallenti effettivamente l’atomo, è necessario che venga assorbito. Secondo la teoria basata sull’equazione di Schrödinger (si proprio lui Billy, quello del gatto), un fotone è assorbito da un atomo solo e soltanto quando ha la giusta frequenza, pari al salto tra i livelli energetici atomici, non un pizzico di più, non un pizzico di meno:

$$\omega_{0}=\frac{E_{f}-E_{i}}{\hbar}s=4$$

Questo risultato deriva dallo studio dell’interazione quantistica tra radiazione e materia, basata sulla teoria delle piccole perturbazioni dipendenti dal tempo in approssimazione di dipolo. Ma non spaventarti Billy, questa è una definizione altisonante e spaventosa che può essere riassunta in modo esaustivo ed elegante con la regola d’oro di Fermi:

$$\omega_{if}=\frac{2\pi\left|L_{fi}\right|^{2}\delta(E_{f}-E_{i}-\omega\hbar)}{\hbar}s=4$$

(L_fi è detto elemento di matrice: tranquillo Billy, serve a dire che il mondo non esploderà).

Questa relazione esprime la probabilità per unità di tempo che un elettrone all’interno di un atomo transisca da uno stato iniziale a uno finale. Essendo presente δ, per le proprietà della Delta di Dirac, esiste una probabilità diversa da zero affinché il sistema atomico passi da uno stato all’altro solo se il suo argomento è nullo, quindi se la differenza in energia tra essi è pari alla pulsazione dell’onda moltiplicata per ℏ, cioè proprio la condizione scritta precedentemente. Ciò è valido per gli stati stazionari, che in quanto tali rimangono inalterati per un tempo indefinito, a meno che non intervengano perturbazioni esterne. Insomma Billy, a meno che tu non gli faccia il solletico, lo stato non cambia forever.

In accordo con il principio di indeterminazione di Heisenberg (no Billy, non quello che sintetizza met in un camper in mezzo al deserto, quello vero) nella forma energia-tempo,

∆E∆t≥ℏ/2

per Δt→∞ (stato stazionario) si ha ΔE→0 quindi la larghezza del livello energetico è nulla e si ha una Delta di Dirac. Quindi come dici sempre tu Billy, “i torni contano”.

Tuttavia, mio caro, c’è un “ma”. So che adori gli imprevisti.

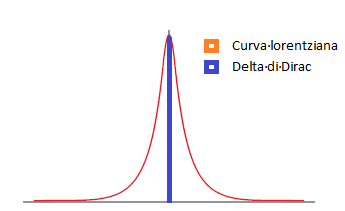
Questo infatti è vero solo per lo stato fondamentale (la configurazione più stabile per un atomo), mentre gli stati eccitati decadono, con un tempo Δt=10^-8 secondi verso stati a energia minore emettendo un fotone, anche in assenza di perturbazioni esterne (emissione spontanea). A questo punto per Heisenberg la larghezza della curva non è più nulla! Infatti Δt≠∞ implica ΔE≠0. Non si ha più una Delta di Dirac ma una curva lorentziana. Abbi pazienza che adesso ti spiego: la transizione è possibile non solo in corrispondenza di un unico e esatto valore della pulsazione ω_0, ma all’interno di un range di valori centrato in ω_0, seppur piuttosto ristretto.

Torniamo ora al nostro gas. La particella viene rallentata solo se il fotone che la colpisce si muove nel verso opposto. In un gas però ovviamente le particelle si spostano in modo del tutto casuale, ci sono cioè atomi in moto anche nel verso concorde a quello del laser. Statisticamente metà degli atomi sono rallentati e metà accelerati e non si ha nessun raffreddamento. La soluzione sta proprio nel fatto che la riga di assorbimento non è una Delta di Dirac ma una Lorentziana. Si inviano sugli atomi due fasci laser diretti in verso opposto, con frequenza ωL leggermente minore della frequenza propria ω0 del sistema atomico. (Sarà necessaria una coppia di laser per ogni dimensione).

A questo punto entra in gioco l’effetto Doppler. Sì Billy, il mistero si infittisce. L’effetto Doppler è un fenomeno estremamente interessante, è il responsabile dell’oscillazione della sirena di un’ambulanza da un tono più acuto a un tono più grave per intenderci. Meriterebbe un articolo a parte, ma in questo caso tentiamo di descriverlo in modo chiaro e semplice.

L'effetto Doppler è un cambiamento apparente della frequenza di un'onda percepita da un osservatore che si trova in movimento rispetto alla sorgente delle onde. In particolare la frequenza percepita risulta maggiore di quella effettiva se l’osservatore si avvicina alla sorgente, minore se si allontana. Facendo riferimento per esempio alla sirena dell’ambulanza, nel prima caso il tono è più acuto, nel secondo più grave.

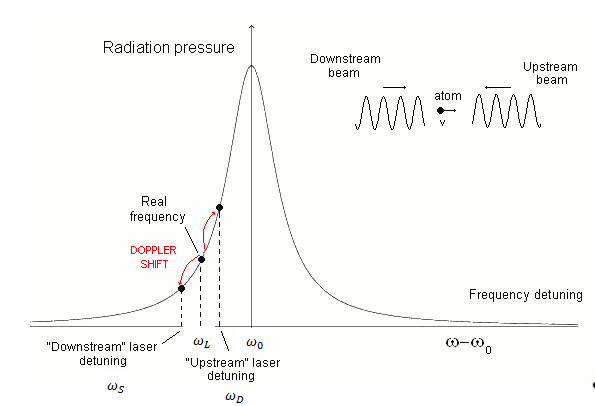
A causa dell’effetto Doppler un atomo in moto per esempio verso destra vede arrivare le due onde dei laser con frequenza diversa, ω_D e ω_S, rispettivamente maggiore e minore di quella emessa ω_L, cui corrisponde una diversa probabilità di transizione e quindi un diverso assorbimento. In questo caso ω_D è più simile a ω_0 pertanto i fotoni che arrivano da destra sono assorbiti di più di quelli che arrivano da sinistra: il loro effetto frenante prevale su quello accelerante e l’atomo rallenta. Il ragionamento è speculare per le particelle che si spostano verso sinistra, per cui l’effetto complessivo è quello desiderato: alleluia alleuia, habemus gas freddum!

Uno dei migliori risultati in questo campo è stato il raffreddamento di elio fino a temperature dell’ordine di 10^-7 K, corrispondenti a velocità di 0.02 m/s. Per questi studi nel 1997 è stato assegnato il premio Nobel per la Fisica a Chu (salute Billy!), Cohen-Tannoudji e Phillips.

Perché hai quella faccia Billy? Non dirmi che ti si è ghiacciato il cervello…