Principio d'indeterminazione

Billy niente fronzoli e gingilli quest’oggi! Nuovo anno (scolastico), per cui si presuppone che tu abbia raggiunto un livello di conoscenza superiore. Per farla breve è arrivato il tempo di passare ad argomenti assai più difficili. Ma come dicevo non perdiamo tempo, perché la conoscenza che acquisirai da quest’articolo manderà i tuoi neuroni in brodo di giuggiole.

Oggi per cena: principio d'indeterminazione!

Nel 1927 questo simpatico giovincello tedesco, per gli amici Werner Heisenberg (inchinati Billy al suo cospetto solo a sentirne il nome), ebbe un’idea del tutto originale. Fino a quel momento l’interpretazione atomistica più accreditata era stata quella planetaria, che tutt’ora è utilizzata per dare un'idea semplificata della materia. Ci sono protoni e neutroni all’interno di un nucleo che gioiosamente condividono emozioni, mentre il terzo incomodo, l’elettrone, essendogli stato vietato un “ménage à trois” è costretto ad orbitare nervosamente intorno a loro.

Heisemberg, da vero uomo tedesco con in una mano la leberknodelsuppe e nell’altra un grosso cucchiaio,  si schiantò contro questa teoria, essendo consapevole che l’unica cosa di cui si era a

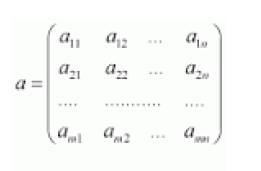
conoscenza a proposito di atomi erano le frequenze emesse, dagli atomi stessi, in particolari fenomeni. Allora dopo aver mandato al diavolo tutti i modelli atomistici, mise al loro posto delle matrici quadrate numeriche.

Billy posso immaginare che probabilmente tu non ne abbia mai sentito parlare, ma per farla semplice immaginale come dei sudoku enormi; infatti almeno teoricamente i numeri all’interno possono arrivare all’infinito. Certo le regole sono un po’ diverse rispetto al gioco orientale, ma non è il momento di parlarne.

La gioia di quest’uomo fu quella di fare parecchi calcoli ed arrivare però ad una formula di estensione insignificante:

Ma con un’immensità d’informazioni al suo interno. D’altronde è nella botte piccola che c’è il vino buono.

Prima di spiegare cosa sono quei triangoli, le lettere e tutto il resto facciamo un grande balzo indietro nella cronistoria. Da quando Newton scoprì quanto fosse divertente trastullarsi con le mele… ma Billy a cosa stai pensando, mi meraviglio di te. Intendevo “da quando furono sviluppate le leggi della meccanica classica” siamo tutti consapevoli che guardando una mela (o un qualsiasi altro oggetto), conoscendo le forze agenti e le condizioni iniziali (velocità e posizione) siamo in grado di calcolare esattamente la traiettoria, cioè la posizione in ogni istante di tempo.

Successivamente a causa della meccanica quantistica, quanto enunciato divenne irrilevante ed alcuni livelli di Angry Birds divennero talmente complicati che nessuno riuscì a superarli con tre stelle! Ed è praticamente tutta colpa di Heisenberg. La formula precedente spiega infatti come non sia possibile contemporaneamente conoscere, o meglio misurare, la posizione e la quantità di moto (che è correlata alla velocità) di una particella. Perdendo così quelle che sono le condizioni iniziali, sarà impossibile determinare la traiettoria dell’oggetto e gli uccellini di Angry Birds colpiranno tutto tranne quello che avevi preventivato Billy.

Come ben sai, però, la meccanica quantistica che regge tutto ciò, diventa rilevante solo quando si trattano corpi infinitamente piccoli, particelle insomma. Quindi forse non è applicabile a degli uccellini. (Sarò io un po’ incapace? Questo non voglio crederlo).

Continuiamo. La formula trascritta letteralmente dice che l'incertezza della posizione (Δx) moltiplicata per l’incertezza nella quantità di moto (Δp) sarà sempre maggiore o uguale ad un numero, dato dalla costante di Plank (h= 6,6 10^-34 joule*secondo) fratto 4 pi-greco.

Billy ripeto nuovamente e per l'ultima volta:

Il principio dice per cui che non è possibile misurare, contemporaneamente e con precisione arbitraria, la posizione e la velocità di una particella. Nota mio caro che la quantità di moto non è altro che la massa per la velocità di un oggetto.

Essendo la formulazione un prodotto d’incertezze posto maggiore di una quantità prestabilita, si deduce che tanto più sarà la precisione con cui si misura una delle due grandezze tanto più grande sarà l’incertezza nella misura della seconda.

A questo punto per capire il perché di ciò devi credermi su quello che sto per dirti.

Ogni particella presenta intrinsecamente una natura ondulatoria.

Puoi anche non credermi ma in quel caso devi andare a consultare tutti gli esperimenti che furono svolti nel novecento e che misero in evidenza questa certezza sperimentale. Non so quanto ti convenga, Billy! Praticamente come sai la luce oltre ad essere un’onda elettromagnetica è anche un insieme di fotoni.  Analogamente anche le particelle presentano natura ondulatoria (ipotesi di De Broglie), sono in pratica sia onde che particelle, per cui a seconda dei fenomeni studiati verranno messe in evidenza le proprietà di una o dell’altra natura.

Ora per spiegarti il principio d’indeterminazione procederò per step successivi a difficoltà crescente. Per cui quanto ti sentirai saturo di scienza potrai interrompere le lettura.

La spiegazione semplicistica di tutto ciò sta nel fatto che quando si osserva una particella, l’atto stesso dell’osservazione porta ad un'incertezza nelle misure nel caso di corpi infinitamente piccoli. Infatti, il semplice gesto del guardare, implica necessariamente la proiezione di in fascio di luce sui corpi. La luce è composta da quest’insieme di fotoni i quali andranno ad interagire con gli oggetti per mezzo di urti, modificando le condizioni in cui la particella, prima della misurazione, si trovava; facendo perdere del tutto quello che è la certezza nella misura. Il concetto di traiettoria diventa in meccanica quantistica non più indispensabile.

Se a questo punto però consideriamo la natura ondulatoria della materia, possiamo arrivare al principio d’indeterminazione partendo dal mondo comune. Ci riconduciamo infatti alle onde più conosciute del mondo: quelle sonore.

Billy, se ti fosse chiesto di individuare una nota musicale ascoltandola per un istante davvero piccolo, a meno che la dea bendata non ti accompagni nella scelta, la risposta sarebbe sicuramente sbagliata. Infatti, con istante, intendo davvero un punto preciso nell’oscillazione della corda che produce la nota. E per  comprendere ed individuare una nota devi per lo meno “ascoltarla” in un periodo della sua oscillazione. Questo ti dimostra come quando il tempo è esatto c’è un’indeterminazione elevatissima nella nota. Analogamente se facessi aumentare il periodo di tempo di ascolto andando così ad incrementare quella che l’incertezza nella variabile tempo, diminuirebbe l’incertezza nella nota.

Riconducendoci al caso elettromagnetico e sostituendo al posto di “nota” --> "posizione" e al posto di “tempo”--> "quantità di moto", ecco che si ritorna al principio d’indeterminazione come enunciato inizialmente.

A questo punto costituiamo un esperimento. Ipotizziamo di studiare il moto di alcune particelle attraverso una fenditura. Il fenomeno che si osserverà, se facciamo in modo che la fenditura abbia dimensione comparabile con la lunghezza d’onda delle particelle, è la diffrazione!

Ricordi Billy? Le particelle hanno anche comportamento di onda a seconda dei fenomeni studiati. Questo è uno di quelli. Il fenomeno di diffrazione è un comportamento peculiare delle onde per cui, quando appunto esse incontreranno una fenditura la cui ampiezza sia simile alla loro lunghezza d’onda, subiranno una deviazione della propria traiettoria.

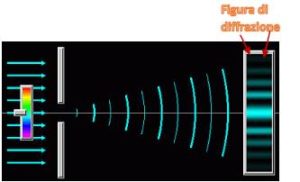
L’immagine mette in evidenza il fenomeno. Non conoscendolo infatti si potrebbe immaginare che facendo incidere un fascio di onde (freccette azzurre), l’immagine che si potrebbe ottenere su uno schermo posto ad una determinata distanza dovrebbe essere un'unica banda di luce posta in corrispondenza della fenditura. Così non è Billy. Puoi vedere come infatti si venga a creare una figura, detta appunto di diffrazione, in cui frange luminose sono alternate da picchi oscuri.

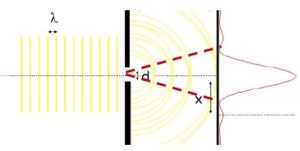
Per definire meglio la situazione d’ora i poi considereremo solo il picco principale quello definito per mezzo delle linee rosse tratteggiate. Ipotizzando che l’intensità dei picchi successivi sia molto minore di quella del principale, per cui irrilevante. L’angolo che si viene a costituire sarà chiamato d’ora in poi “θ”, “ʎ” sarà la lunghezza d’onda della particella ed infine “d” indicherà la spaziatura della fenditura.

Per le leggi sulla diffrazione sappiamo che

Δθ≈λ/d

Niente di più facile Billy! Per diminuire l’incertezza nella posizione si deve diminuire θ. Facendo ciò infatti anche la larghezza del picco tenderebbe a diminuire, e per noi sarebbe più semplice individuare dove l’onda e di conseguenza la particella va a schiantarsi. Questo si può ottenere diminuendo la lunghezza d’onda ʎ.

Contemporaneamente però, poiché la quantità di moto di un’onda e di conseguenza della particella ad essa associata è data da

Δp=h/λ

(Dove h ti ricordo essere la costante di Plank, p è la quantità di moto e ʎ la lunghezza d’onda), diminuendo ʎ avremmo sì una migliore certezza nella posizione, ma allo stesso tempo un’incertezza maggiore nella quantità di moto. Ed eccoci di nuovo al principio d’indeterminazione: aumentando la precisione nella posizione abbiamo perso informazioni riguardanti la quantità di moto.

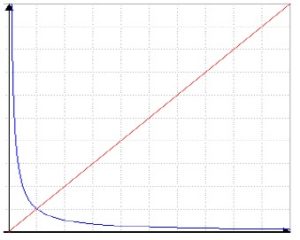
Il grafico mostra l’andamento qualitativo di quanto appena detto. Se sull’asse orizzontale si pone la lunghezza d’onda ʎ la linea rossa indicherà il Δθ mentre il ramo d’iperbole Δp.  All’aumentare di lambda la retta aumenterà sempre di più mentre la linea blu diminuirà. Per cui l’incertezza nella posizione tenderà ad aumentare mentre l’incertezza nella quantità di moto tenderà sempre più a zero e viceversa

Bravo Billy se sei riuscito ad arrivare fino a questo punto, meriti un croccantino! No non ti sto dando del cane o peggio della cagna… ma credo fortemente nel condizionamento positivo!

In realtà quanto detto non è altro che la forma più specifica del principio d’indeterminazione, infatti secondo Heisenberg lo stesso avviene per varie coppie di grandezze come energia e tempo ed in generale per un gran numero di osservabili fisiche. Per cui non sarà mai possibile conoscere contemporaneamente tutte le proprietà di un oggetto. Ciò porta ad un'amara consapevolezza. L’osservazione di ciò che ci circonda non è altro che frutto di un insieme di probabilità. Come lo stesso Heisemberg definisce nel suo libro "fisica e filosofia", si arriva ad un'implicazione: la conoscenza di un dato fenomeno non sarà mai oggettiva, completa ed imparziale. A meno che l’osservatore non riesca ad essere consapevole di come egli influisca sulle osservazioni. Il tipo di conoscenza che ne deriva è per cui  di tipo probabilistico.

Ma come terminare senza citare il grande uomo dai baffi bianchi in questo caso?
Einstein rifiuta l’idea che ci si debba accontentare di semplice probabilità.

D’altronde non è possibile che il vecchio lassù giochi a dadi! La fisica non è un gioco d’azzardo. Devono sicuramente mancare alcuni concetti che ancora non conosciamo

Billy, veritas filia temporis.