Il tutto è maggiore della somma delle parti

Il tutto è maggiore della somma delle parti

diceva Aristotele. Mai sentito parlare di sistemi complessi?

Dall'andamento dei mercati, alle relazioni sociali; dall'evoluzione di una malattia, all'imprevedibilità del tempo atmosferico; dai laser, all’improvvisa insorgenza di una crisi epilettica, tutti questi sistemi all'apparenza assai diversi tra loro, hanno la proprietà d'esser complessi.

Sarebbe difficile immaginare una società così evoluta come la nostra, in grado di spedire sonde oltre l’orbita del sistema solare (vedi "The pale blue dot") ma incapace di prevedere che tempo farà domani, no?

Eppure è così.

Debbo ammettere che, per quanto sia importante a livello “strumentale”,  l’esempio delle previsioni meteo non rende giustizia alla raffinatezza concettuale dell’argomento che stiamo trattando:  oltre al potere strumentale, vi sono grandi implicazioni filosofiche ed epistemologiche che trovano nella teoria della complessità il proprio filo conduttore. Spesso, in questa breve finestra sul tema, mi capiterà di lambire gli argomenti più disparati, talvolta nominandoli soltanto senza possibilità di completezza, a prova del fatto che la scienza della complessità si dispiega in ogni ambito, fornendo un potentissimo strumento per capire il mondo circostante.

Basta questo per renderla degna di attenzione, ma direi di andare avanti, procedendo gradualmente.

SISTEMI COMPLESSI

Stuart Kauffman è professore di biochimica all’Università di Pennsylvania e si occupa di sistemi adattativi complessi.

In un'intervista a La Stampa, diceva:

• Perché uno stormo di uccelli vola in un certo ordine?
• Come si sviluppa una colonia di batteri in un ambiente?
• Come si scopre qual è la tecnologia vincente tra un insieme di tecnologie concorrenti che si propongono di risolvere lo stesso problema?
• Come si spiega il funzionamento della borsa?

Tutti questi problemi sono accomunati da alcuni elementi: ci sono individui che interagiscono (molecole, batteri, uccelli, macchine, ma anche fotoni, esseri umani!); ci sono regole che gli individui seguono; ci sono interazioni tra un individuo e l’altro; ci sono percorsi di adattamento ai cambiamenti esterni.

In pratica, non si può comprendere il volo di uno stormo di uccelli studiando il comportamento individuale di un uccello: ogni uccello segue regole, interagisce con gli altri uccelli, produce un sistema che si muove in modo ordinato e in questo modo si adatta ai mutamenti esterni. Visto dall’ esterno un sistema può avere un comportamento apparentemente casuale, ma comprendendone le regole di fondo e definendole in termini matematici quel comportamento diventa relativamente prevedibile. E quindi migliorabile.

Per chi volesse godersi lo spettacolo, ne propongo una versione filmata a Roma.

E non è tutto: sistemi che, considerati nella loro forma macroscopica, hanno comportamenti ordinati, possono esser frutto di dinamiche del tutto aleatorie a livello microscopico.

La  foto, che ho scattato (da smartphone) dopo aver osservato (in slow motion, per quel poco che concede un telefono!) la diffusione di alcuni fluidi in acqua (ok, l'olio in sospensione è solo per far scena!) è un esempio di quanto appena detto.

Il fenomeno della diffusione , ovvero il mescolamento  di sostanze senza l’intervento di moti convettivi, ci mostra come, pur partendo da dinamiche di natura aleatoria (random walk) per le particelle microscopiche della sostanza che diffonde, si ottiene un moto ordinato nel considerare il sistema macroscopico che ne scaturisce.

Altrettanto curiosa è la similitudine tra il processo fisico della goccia nel bicchiere e l'algoritmo con il quale Google , almeno fino a qualche anno fa, operava per portarvi alle pagine da voi desiderate. Il modello, che pure non é (troppo) difficile, è un po' tecnico, e non voglio confondervi le idee.

Per chi fosse curioso, però, ecco il link.

TORNANDO A NOI

Dopo alcuni esempi di cui è facile fare esperienza (stormi, diffusione, interazioni sociali) spero di aver catturato abbastanza l’attenzione del lettore per entrare nel vivo del discorso: cos’è la tanto citata complessità?

I fenomeni in questione, così come quasi tutti gli altri meccanismi naturali, sono detti sistemi complessi. La parola «complessi» è stata evidenziata perché va intesa come termine tecnico, che risponde ad una ben precisa, rigorosa definizione e non significa semplicemente «complicato». Il mondo fisico è colmo di problemi complessi ma non complicati: un esempio è il doppio pendolo mostrato nel video che segue.

Cosa succede ed in cosa questo sistema apparentemente semplice è classificabile come complesso?

Nel video si vedono 2 pendoli doppi identici; sembra partano dallo stesso punto, seguendo gli stessi percorsi eppure , col passare del tempo, finiscono per percorrere traiettorie del tutto differenti. Perchè?

La risposta sta negli angoli da cui partono i due pendoli: per quello di sinistra è di 130°, mentre in quello di destra è 129°. La differenza nelle condizioni iniziali (è così che si chiamano) è minima, eppure, col passare del tempo, i 2 sistemi evolvono portando ad esisti completamente diversi: ecco un esempio di sistema complesso caotico. Un sistema che, da lievi differenze nel suo stato iniziale, può evolvere in maniere estremamente diverse.

Sebbene segua leggi deterministiche, esso rimane quasi del tutto imprevedibile: eppure è così semplice! Ora estendiamo il discorso a migliaia, milioni, miliardi di miliardi di variabili (altro che due soltanto!) ed otteniamo (i modelli de) l'atmosfera, la società, il corpo umano, i moti diffusivi dei fluidi, etc.

Capiamo subito che un sistema complesso esibisce una sensibilità esponenziale rispetto alle condizioni iniziali. Il celebre effetto farfalla ne è un esempio:

Un battito d’ali in Texas può generare un uragano in Brasile.

Parafrasando, una impercettibile perturbazione del sistema allo stato iniziale, quale è lo spostamento d’aria causato dal battito d’ali di farfalla, produce conseguenze macroscopiche (un uragano) al termine dell’osservazione.

Invero non basta questo per poter definire ‘caotico’ un sistema complesso: vi sono altre proprietà necessarie, che però non verranno discusse in questo articolo.

Per amor di completezza, potremmo dire quanto segue: le principali caratteristiche che sono state associate alla complessità riguardano, oltre alla forte dipendenza dalle condizioni iniziali, la presenza di numerosi elementi interagenti, la non linearità delle interazioni , la comparsa a livello globale di proprietà emergenti prive di un analogo microscopico, e non ultima la capacità di auto-organizzazione: il volo degli uccelli vi dice qualcosa? E la vostra coscienza, da intendersi come proprietà emergente, inspiegabile a partire dal funzionamento del singolo neurone, invece? Il titolo dell'articolo dovrebbe iniziare ad essere meno opaco.
A meno di non affidarsi alla religione, al misticismo o alla metafisica, la coscienza -un qualcosa che è più facile da nominare che da definire- è un sottoprodotto del cervello,  un altro esempio di sistema complesso.

Va aggiunto che di cosa sia la coscienza sappiamo ben poco (checché ne dicano alcuni psicologi dell’ultima ora): ciò non toglie che la strada intrapresa, e cioè il tentativo di indagarne le dinamiche con il rigore delle scienze fisiche, è incoraggiante, oltre che profondamente significativo. Agli albori, la fisica prediligeva una modellizzazione in forma chiusa, atta a semplificare quanto più possibile l’oggetto di indagine. Oggi vediamo che le scienze biologiche e fisiche sono caratterizzate da una crisi della spiegazione semplice: quelli che sembravano essere i residui non scientifici delle scienze umane (l’incertezza, il disordine, la contraddizione, la pluralità, la complicazione, ecc.) fanno oggi parte della problematica di fondo della conoscenza scientifica, contribuendo al processo di riconciliazione tra hard science e soft science.

Questa considerazione ‘storica’ ci pone davanti a un’evidenza: la fisica dei sistemi complessi è giovane. Lo studio della dinamica dei sistemi complessi è reso oggi possibile dalla disponibilità di elevata potenza di calcolo dei moderni computer. Per molti anni è stato difficile studiare il comportamento dei fenomeni complessi perché i modelli usati per descriverli erano così difficili che la principale modalità computazionale usata, rappresentata dall’integrazione di equazioni differenziali, comportava tempi di calcolo estremamente elevati.

Soltanto grazie alle moderne tecniche di simulazione computerizzata è possibile studiare l’evoluzione di sistemi a molti corpi.

In proposito, molti conosceranno Life, il gioco inventato dal matematico John Conway.

Chi non lo conoscesse, è invitato a provarlo: è semplice (le poche regole le trovate qui) ed istruttivo.

E’ un esempio di sistema complesso, nato come gioco, che ha portato allo sviluppo della teoria degli automi cellulari. Secondo questo modello, un sistema viene rappresentato come composto da tante semplici parti ed ognuna di queste parti evolve conformemente ad una propria regola interna ed interagisce solo con le parti ad essa vicine. L’evoluzione globale del sistema emerge dalle evoluzioni di tutte le parti elementari.

Gli stati di tutte le celle sono aggiornati contemporaneamente in maniera sincrona: un automa cellulare è perciò un sistema dinamico discreto in quanto spazio, tempo e stati del sistema sono discreti; ne esistono anche di continui.

Ogni elemento dell’automa in una griglia spaziale regolare è detto cella e può essere in uno degli stati finiti che la cella può avere. Gli stati delle celle variano secondo una regola locale, cioè lo stato di una cella ad un dato istante di tempo dipende dallo stato della cella stessa e dagli stati delle celle vicine all’istante precedente.

Al netto, le regole sono molto semplici, ma i singoli elementi, liberi di muoversi su una griglia che rappresenta il loro universo, creano situazioni imprevedibili. Non siamo in grado di predire il comportamento di ogni singolo elemento, possiamo soltanto prevedere una serie di stati possibili, non quello preciso che ne risulterà. Imprevedibile non a caso come la vita umana, che di regole ne ha tantissime, di cui conosciamo una porzione limitata: nessuno può sapere cosa ci accadrà domani, malgrado i tentativi di dominare il futuro in termini probabilistici (occhio alle assicurazioni!).

Al prossimo religioso che fa pronostici sul vostro domani, al prossimo curatore miracoloso, al prossimo politico che vi propone soluzioni semplicistiche e totalizzanti, rinfrescategli la memoria: dalla complessità non si sfugge. I meccanismi di persistenza, retroazione ed autoalimentazione, in  grado di amplificare rapidamente gli effetti di perturbazioni quali una modifica durante la simulazione, sono la manifestazione della non linearità. E nell’affrontare i problemi più ricurvi con idee semplici e lineari, si prendono le migliori cantonate (i merluzzi ne sanno qualcosa: continua e lo saprai anche tu!).

TRANSIZIONI DI FASE

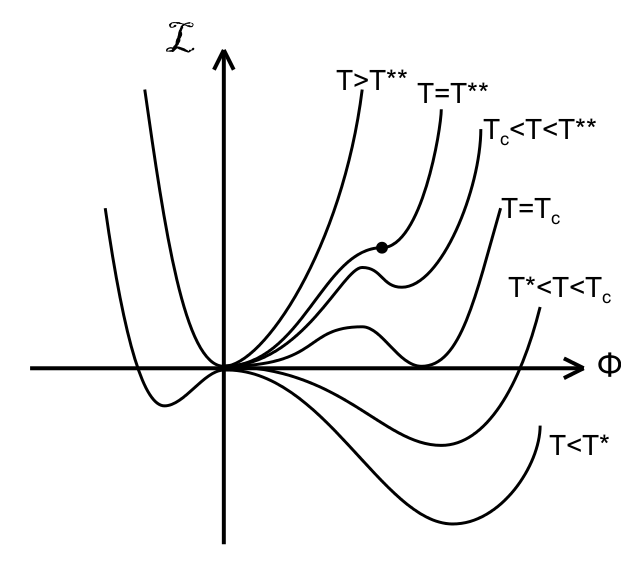
Avviandoci verso la conclusione, un tema interessante, spesso trattato con gli strumenti ivi discussi, è quello delle transizioni di fase. A chiunque abbia frequentato un liceo verranno in mente i passaggi di stato della materia: da liquido a solido ad esempio. In effetti sono un esempio di transizione di fase.  Esse sono bruschi cambiamenti qualitativi nel comportamento collettivo di un sistema fisico, che avvengono senza che vi sia nessun cambiamento nelle interazioni fra i costituenti elementari.

Personalmente trovo più intriganti le transizioni di fase applicate alle dinamiche sociali, che potrebbero modellizzare numerosi fenomeni cooperativi del passato (penso alle isterie collettive durante il nazismo) e del presente (come i fenomeni migratori o i Family Day), ponendo le basi -perché no- per previsioni future atte a scongiurare o, quanto meno, ad attenuare catastrofi geo-politiche e finanziarie. Sebbene quest’ultimo sia uno spunto (e come tale va preso!) e malgrado il caso ci metta il suo zampino, mi piace sottolineare che non è fantascienza.

Tornando coi piedi ben saldi al suolo , si pensi ad esempio ad una transizione di fase come quella da acqua a ghiaccio, che avviene (a temperature inferiori al punto di congelamento) quando fluttuazioni locali danno origine ad una regione solida abbastanza grande da far sì che il guadagno in energia libera, associato alla formazione della fase solida, superi il costo energetico relativo alla formazione di una interfaccia fra le due fasi: questa regione risulta quindi stabile e funge da nucleo di condensazione per ulteriori accrescimenti, mentre una analoga regione solida, di dimensioni inferiori, sarebbe condannata alla scomparsa. Una singolarità, insomma, che ha per effetto un fenomeno macroscopicamente percepibile.

L’esempio, nella sua semplicità concettuale, è paradigmatico: qualcosa di simile, per mezzo di singolarità, avviene in molti altri sistemi complessi. Non di meno in quelli biologici.

La biologia contemporanea considera ogni specie vivente come una singolarità, che produce singolarità. La vita stessa è una singolarità, all’interno dei vari tipi di organizzazioni fisico-chimiche esistenti. Ed è con un aneddoto "biologico-sociale" che concludo : prometto, in queste ultime righe, di fornirvi un’argomentazione solida e convincente da usare con semplificatori e populisti d’ogni specie.

A voi il giudizio.

AIUTIAMO I MERLUZZI A CASA LORO!

Cosa c'entrano i merluzzi, Lionel Messi, la teoria della complessità ed alcuni politici italiani?

Nel 1992 la pesca dei merluzzi in Canada si è esaurita, e quarantamila pescatori del posto sono rimasti senza lavoro. Quando la pesca del merluzzo crollò, l’industria alimentare del Canada, ormai in crisi, cercò le cause del fenomeno: perché il pesce scompariva? La risposta dei biologi fu: «Cacciate le foche che divorando il pesce». Per tutto il decennio successivo, malgrado una ferocissima strage di foche, il numero di merluzzi continuò a declinare.

La domanda sorge spontanea: perché? Pare la più ovvia soluzione, no?

Non ci sono più merluzzi → Le foche mangiano i merluzzi → Ammazziamo le foche così torneranno i pesci.

E' lineare, così come la catena alimentare. E' ragionevole, ed....errato. La conseguenza di questo ingenuo (anche se apparentemente ovvio) modo di ragionare, fu che la pesca del merluzzo nel nord Atlantico, da allora, non si è mai più ripresa.

L'errore sta nel considerare lineare un fenomeno che non lo è affatto, quale l'intricata rete alimentare marittima.

Si scoprì, infatti, che la foca, oltre che a cibarsi del merluzzo, si nutriva anche di altri pesci, a loro volta predatori del merluzzo: venute meno le foche, questi ultimi proliferarono e segnarono il declino dei poveri pesciolini. Si era trattato in maniera lineare un sistema complesso, che di per sé è più simile ad una rete, che non ad una linea diritta. D'altronde «rete» è termine preso in prestito dalla pesca: un intrecciarsi di nodi e corde che li congiungono. L’errore dei canadesi era proprio di «rete», stavolta nel senso di «network»: guardando solo al legame vorace tra foche e merluzzi avevano dimenticato che la catena alimentare non è una linea, ma un reticolo, dove decine di predatori interagiscono.

La «network theory», è uno strumento affascinante di analisi e predizione che si presta alla descrizione dei fenomeni complessi quali la società, la diffusione di malattie, i fenomeni migratori, i meccanismi di assegnazione del credito tra banche durante una crisi economica, internet, etc : servizi segreti, scienziati,  giornalisti e politici la usano, influenzando la nostra vita quotidiana; eppure pochi di noi sanno esattamente cosa sia e quali regole e algoritmi la governino.

In due parole possiamo immaginarla come il modo di descrivere fenomeni complessi attraverso un reticolo in cui i nodi rappresentano i soggetti coinvolti ed i link tra i vari nodi, le relazioni tra di loro. I nodi, rappresentabili da pallini, possono avere "importanza" diversa a seconda di quante relazioni hanno con gli altri nodi della stessa rete.

Per una breve introduzione storica, rimando il lettore alla vicenda dei "Sette ponti di Königsberg" e, nel frattempo, procedo con un esempio più attuale: perchè Lionel Messi è un asso strepitoso nel Barcellona e solo "buon giocatore" nella Nazionale argentina?

La spiegazione non si trova nel diverso valore tecnico dei compagni, ma nei diversi rapporti di «rete» che il numero 10 intrattiene con loro. Se i giocatori sono "i nodi" della rete che chiamiamo "squadra", nel Barcellona Messi è un "nodo importante", la palla gli arriva sempre (ovvero è un nodo collegato con tutti gli altri), mentre in Nazionale è il migliore, ma non il fulcro (ha meno link con gli altri giocatori),e la giocata deve conquistarsela.

L'applicazione di questi modelli è fondamentale per una migliore comprensione della complessità del mondo circostante.

Forse è per questo che bisogna diffidare dello spirito demagogico, anche se apparentemente ragionevole, di buona parte dell'attuale classe politica, specie sul tema che risuona di testata in testata negli ultimi tempi: l'immigrazione.

Sempre più spesso si sentono dichiarazioni semplicistiche e soluzioni totalizzanti: dall'accoglienza incondizionata della sinistra, rispetto ad un fenomeno che non sa gestire, alle idiozie della destra più ignorante che continua a proporre l'utopia dello "aiutiamoli a casa loro".

Dal buonismo sinistroide, che finisce soltanto per alimentare le tensioni sociali e la guerra tra poveri, alla miopia conservatrice, che crede di dover fare la guerra per fermare l'immigrazione.

L'episodio delle foche è paradigmatico: applicare soluzioni lineari e "ragionevoli" a realtà complesse e caotiche è squisitamente una cazzata.

Non cadete in rete: almeno non in quel senso!