Sono fuori dal tunnel (o L'effetto tunnel quantistico)

Ciao Billy! Oggi ti scrivo anche io. Perché?

Ho visto il blog: il titolo è figo, la gente che scrive sembra figa ma soprattutto l’idea è supergeniale. Ho sempre creduto che parlare di scienza debba essere qualcosa di facile e intuitivo, mio caro. Dovrebbe essere facile come raccontare una puntata di Beautiful a mia nonna (naturalmente con le dovute semplificazioni), lasciando a chi di dovere il rigore matematico e tutte le derivazioni di equazioni assurde e con simboli! e perché allora non dare anche io il mio contributo? Ti voglio raccontare una cosa stra-bellissima.

Fai la pipì prima perché l’emozione potrebbe essere troppa, da indurti a fartela addosso.

L'effetto tunnel

Billy oggi ti racconto l’effetto tunnel! Parlando di cose molto strane ti avviso che tutto quello in cui credi potrebbe essere stravolto. Per farti capire, ti consiglio di immedesimarti. Chiudi gli occhi e immagina di essere particella. Fatto?

Ecco perfetto. Si ma lascia perdere le particelle quantistiche non m’interessa che ti piace sentirti un gluone o un gravitione. Vola basso. Immaginati una pallina di carta. Una pallina di carta piena di coscienza e voglia di fare. Prendendo ora una gran rincorsa, pensa di schiantarti contro una parete. Se le scienze stocastiche sono dalla tua parte: ta-dam! In men che non si dica ti ritroverai al di là della parete senza nemmeno un graffio. L’effetto tunnel dice proprio questo: una particella con una massa e una determinata energia avrà una probabilità di fare tunnel, cioè di attraversare una barriera energetica.

In realtà, Billy non voglio deluderti ma la probabilità che tu riesca a superarla senza sbatterci contro è molto bassa.

Ipotizziamo che tu voglia superare una parete di superficie 1 metro quadro, al cui interno sono presenti un sacco di atomi ( se consideriamo una parete fatta unicamente di atomi di carbonio te ne servirebbero più di un miliardo, sapresti dove trovarli?), continuiamo ipotizzando che la tua massa per quanto piccola possa essere sia di un grammo cosi da vederti mentre ti schianti verso la parete... Ehm così possiamo vedere mentre attraversi la parete!

Visto che stiamo ragionando per assurdo ipotizziamo che tu sia veloce come il più bravo tra gli umani (Usain Bolt) per cui riesca a raggiungere la velocità di 37 km/h (10,28 m/s). La probabilità che tu riesca a superare la barriera larga 10^{-10} metri (circa 500000 volte più sottile di un tuo capello) è, per darti un valore spannometrico :

$$6\times10^{-45}s=4$$

Billy prendi uno zero piazzaci una virgola altri QUARANTAQUATTRO zeri e poi il numero sei. Credo che non te la prenderei se approssimiamo con zero. Quindi per la sacra scienza probabilistica andrai a schiantarti contro la parete. Ahimè, che disgrazia, spero non ti sia fatto male.

Se la tua scelta fosse stata più furba, se ad esempio avessi voluto immedesimarti in un elettrone e se avessi voluto attraversare una parete energeticamente più accessibile la probabilità sarebbe stata molto più alta! So cosa stai pensando. L’idea della tua immedesimazione è partita da me e quindi avrei potuto dall’inizio fare in modo che riuscissi ad oltrepassare l’ostacolo. Ma caro Billy, tutto questo, era per farti capire che è un fenomeno che non osserverai mai nel mondo macroscopico!

La formula che regge il tutto è:

$$T=\frac{1}{1+V_{b}^{2}(\sinh\beta a)^{2}/[4E(V_{b}-E)]}s=3$$

dove $$V_{b}$$ energia della barriera ed E è energia della particella, che in maniera più semplice qualora voglia considerarsi che la larghezza della barriera sia sufficientemente molto larga diventa:

$$T=\frac{16(V_{b}-E)Ee^{-2\beta\alpha}}{V_{b}}s=3$$

Ma la rozzaggine che contraddistingue il mondo ingegneristico, caro Billy, fa sì che io ti dica l’unica parte importante di tutta la formula:

$$T\varpropto e^{-2\beta\alpha}s=3$$

Billy non andare via ora ti spiego il significato di tutti i termini così che ti renderai conto della magica scienza che ci sta dietro (nota ∝ significa che “il termine è approssimabile a”) :

• T, signor principe della formula rappresenta il coefficiente di trasmissione. Da un valore che rappresenta quale sia la probabilità della particella di fare tunnel attraverso la particella.
• β rappresenta invece un fattore che tiene contemporaneamente conto della massa della particella e della differenza energetica tra barriera e particella
• a infine è la larghezza della buca.

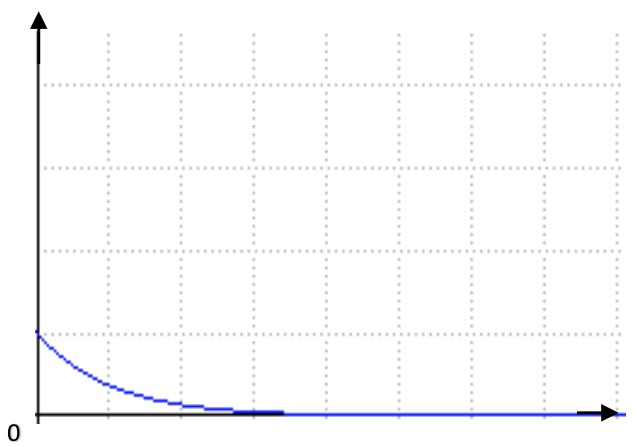
Questo invece caro Billy è l’andamento dell’ultima formula scritta (linea blu). È facile da interpretare anche per chi il giorno non disegna funzioni esponenziali decrescenti (è questo il nome della funzione)! Sull’asse orizzontale vengono scritti i valori dati da 2βa, mentre sull’asse verticale sono rappresentati i valori di T. E’ facile capire che mano a mano si utilizzano valori dell’asse orizzontale più grandi (spostati verso destra) i valori di T tendono sempre più a zero.

Per cui ogni volta che si incrementa β o aumentando la massa della particella o aumentando la differenza di energia tra particella e barriera o si incrementa il valore di a allargando la buca, la probabilità 0 che avvenga effetto tunnel tende mooooooooolto rapidamente a zero! E viceversa.

Ora che conosci anche l’effetto tunnel hai una marcia in più, ma sappi che non ti aiuterà nelle tue uscite di caccia dell’altro sesso, né è un argomento di conversazione del tè delle cinque p.m.!

Caro Billy Prosit!