Il nastro di Möbius e le superfici non orientabili

Sei un discendente di Martin Lutero, studi astronomia con Gauss, sei il primo matematico ad introdurre le coordinate omogenee in geometria proiettiva, divieni professore universitario bruciando tutte le tappe e poi un giorno, mentre magari stai sorseggiando del the, ti accorgi di una cosa che magari ti sembra anche stupida, che però ha un suo fascino. La appunti e un giorno ci scrivi un articolo, come ne hai scritti tanti altri per tante cose molto più complicate.

E di tutto quello che hai fatto nella vita vieni ricordato per quello che sicuramente non avresti scelto tu. Questo è il problema del "ai posteri l'ardua sentenza". I posteri sono il problema. Non i poster, quello dipende dai gusti.

Ancora non hai capito di chi sto parlando? Ma di August Ferdinand Möbius, ovviamente. L'uomo del nastro di Möbius che, per chi non lo sapesse, è l'esempio per eccellenza di una superficie non orientabile.

Scusa Billy, mi sono dimenticato della tua stoltezza. Ora vado piano. Coglione.

Il nastro di Möbius

Il nastro di Möbius si può ottenere con una strisciolina di carta larga qualche centimetro, incollata agli estremi con dopo avergli dato un mezzo giro di torsione.

Con questo semplice gesto avrete creato, come già detto, una superficie non orientabile. Le superfici che nella vita quotidiana siamo abituati ad osservare hanno sempre due facce, per cui percorrendo idealmente uno dei due lati non raggiungiamo mai il secondo. Per queste superfici è possibile stabilire convenzionalmente un lato "superiore" o "inferiore". Per una superficie non orientabile questo non è vero, in quanto percorrendo il nastro lungo una faccia a scelta, dopo un giro ci ritroveremo (disorientati e frastornati) sull'altra.

Per chiarirvi ogni dubbio, seguite una formica di questo video e capirete meglio cosa vuol dire. 

Come sempre, le cose semplici sono le più affascinanti. E il successo di questo scherzo della topologia ha sconfinato tutti i campi delle scienze sforando nella musica, nell'arte, nella letteratura, nella cinematografia e in alcuni trucchi di magia ("bande afgane"). Tra le sue citazioni più famose ho scelto quella di Mauritius Cornelius Escher che potete vedere all'inizio dell'articolo. 

Spero di avervi incuriosito abbastanza, e se così non fosse vi lascio un video che spiega quanti bei trucchetti è possibile fare con qualche striscia di carta sfruttando le caratteristiche di questa figura quasi magica.

Prima di lasciarti alla tua vita di banali superfici orientate lascia che ti dia il colpo di grazia.

Rullo di tamburi, vi presento la bottiglia di Klein.

La bottiglia di Klein

Sì Billy lo so che vuoi vedere subito un'immagine, ma aspetta un attimo. Devo avvisarti che in realtà questa superficie vive nello spazio euclideo quadridimensionale R⁴, quindi non è "umanamente" rappresentabile. Infatti mentre il nastro di Möbius può essere rappresentato all'interno dello spazio tridimensionale, la bottiglia di Klein non può (e infatti nelle rappresentazioni grafiche tridimensionali la superficie è costretta ad autointersecarsi da qualche parte) ma può essere rappresentata nello spazio euclideo quadridimensionale.

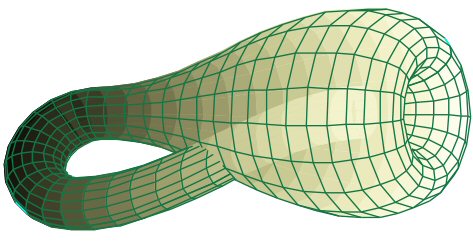
Costruire una bottiglia di Klein è leggermente più difficile, quindi ti lascio la "guida" della buon vecchia Wikipedia.

La bottiglia di Klein può essere costruita (in senso matematico) "incollando" i margini di due nastri di Möbius. Se una bottiglia di Klein è divisa in due lungo il suo piano di simmetria, il risultato è un nastro di Möbius, raffigurato a destra. Si tenga presente che l'intersezione raffigurata non esiste veramente. Infatti è possibile tagliare la bottiglia di Klein in un singolo nastro di Möbius.

Come sempre in questo articolo, ecco un video per visualizzare il tutto:

Se hai visto il video fino in fondo ti sarai accorto di una cosa assurda: tagliando a metà la bottiglia di Klein riotteniamo il nastro di Mobius! Già vi vedo sbrodolare nella nerdaggine, quindi prima che chiudiate l'articolo per andare a tagliare striscioline di carta da incollare vi lascio un ultimo video, il più geniale.

Cosa succede quando una superficie non orientabile incontra il genio compositivo di Bach? Questo.
Ci leggiamo presto Billy!