L'effetto Dzhanibekov, o meglio il teorema della racchetta da tennis

Qualche articolo fa ti abbiamo raccontato di alcuni dei teoremi dai nomi più strampalati, dal teorema della scimmia instancabile a quello della pizza, ti sarai reso conto che matematici e fisici hanno un grande dono quando si tratta di dover dare nomi alle cose.

Perchè non riaprire quella lista con un nuovo e frizzantissimo teorema?
Quello della racchetta da tennis.

Fuorviati dai teoremi dell’analisi matematica, spesso si pensa che questi siano delle verità imperscrutabili ai comuni mortali, che qualche genio di turno tiri di volta in volta fuori dal cappello come un bianconiglio. La realtà è che come spesso accade, l’uomo si è trovato di fronte a qualche fenomeno che ha cercato di comprendere e modellizzare, ovvero riuscire a descrivere con gli strumenti della fisica e della matematica. E quello che fanno gli scienziati da da secoli, osservare il mondo per comprenderlo.

Basta con tutto questo romanticismo, torniamo a noi Billy. Anzi, facciamo un salto nella Madre Russia degli anni ‘60, quando Vladimir Dzhanibekov entra all'università di San Pietroburgo per studiare fisica, ma non trovando un blog che spiegasse in modo simpatico e semplice la fisica (*occhiolino*) decide di dedicarsi all'aviazione. Così nel 1970 viene selezionato per fare l'astronauta e conciano così le sue cinque missioni che gli hanno fatto accumulare per 145 giorni, 15 ore e 56 minuti nello spazio (sono quasi cinque mesi interi). In questa lunga permanenza il nostro amico russo nota che un oggetto a tre assi di rotazione, come un cacciavite a T ad esempio, mostra un comportamento diverso in base all’asse attorno al quale viene messo in rotazione. ((Nel 1991 viene pubblicato per la prima volta il paper scientifico che spiega l’effetto.))

Un respiro profondo e cominciamo.

Il "teorema della racchetta da tennis"

Il momento di inerzia misura l'inerzia del corpo al mutare della sua velocità angolare, praticamente quanto l’oggetto si oppone ad una rotazione. Un corpo a T come quello del nostro cavviavite presenta tre assi di rotazione principale, come in figura((Per comodità utilizzerò delle immagini che sono già sul Web, quindi il nostro magico cacciavite assumerà le sembianze di un satellite per il momento.)):

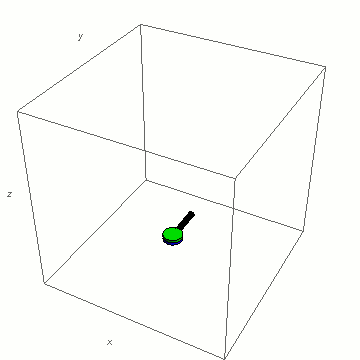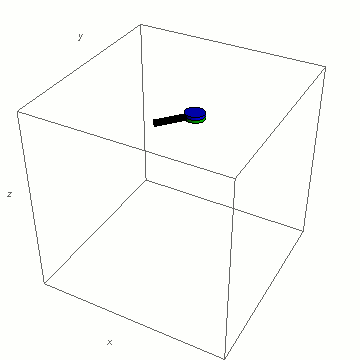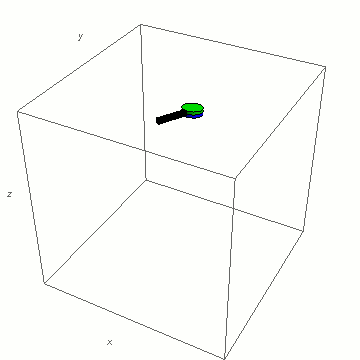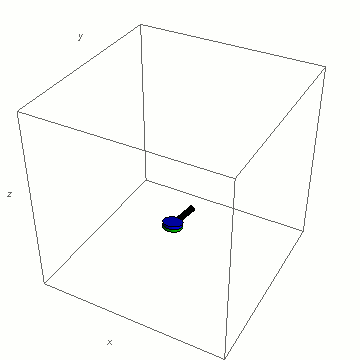
• verde: asse di rotazione con il minore momento di inerzia
• rosso: asse di rotazione con momento di inerzia intermedio
• blu: asse di rotazione con il maggiore momento di inerzia

Mettiamo ora in rotazione il nostro corpo attorno a ciascuno degli assi. ((Ho creato le immagini e le GIF a partire da questo bellissimo video, dagli un’occhiata.))

Cominciamo ad esempio con quello a inerzia maggiore:

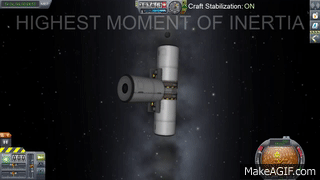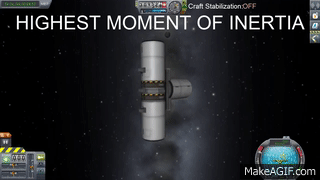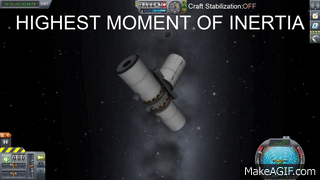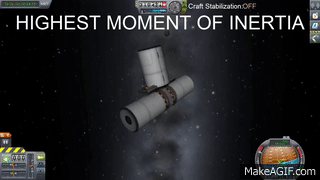
La rotazione è semplicemente stabile, nulla di sorprendente. Proviamo allora con l’asse dal momento di inerzia minore, quello più “facile”:

Niente, tutto funziona come ci si potrebbe aspettare. Quindi cosa dici? Troppa Vodka a bordo per Dzhanibekov? Forse sì, ma non diamoci per vinti, e con gesto di stizza mettiamo in rotazione il nostro cacciavite attorno all’ultimo asse, quello dal momento di inerzia intermedio:

Ah, hai visto anche tu vero? Fa qualche giro, ruota di 180 gradi, qualche altro giro e poi torna a posto. Per ricominciare.

La dimostrazione (che puoi trovare qui) fa vedere come, mentre le rotazioni attorno ai due assi a maggiore e minore momento di inerzia sono governate da delle leggi che ne assicurano la stabilità, attorno all’asse dal momento di inerzia intermedio la velocità di rotazione attorno all’asse ad inerzia maggiore segue una legge instabile, per cui ad il minimo disturbo “esplode” provocando il flip (ribaltamento) del nostro cacciavite.

Tutto molto bello, ma cosa ha a che fare questo con una racchetta da tennis? Beh, tutto. la differenza è che mentre con un cacciavite a T per osservare l’effetto è consigliabile andare qualche chilometro fuori dall’atmosfera terrestre in una base spaziale a microgravità, con una racchetta l’esperimento puoi farlo anche nel tuo garage.

 

Non sempre il mondo si comporta come ci aspettiamo, nevvero?