La geometria dei numeri: i poligonali

Numeri. Strumenti potentissimi, fine invenzione dell'intelletto più razionale che purtroppo (per molti) diventano solo uno dei tanti modi per quantificare la ricchezza. O per tenere il conto della versione dell'iPhone (S e C non sono escluse).

Il mondo dei numeri è un mondo quasi magico, un universo di concatenazioni che spesso mi sconcertano. Pensaci Billy. Un giorno un gruppo di uomini decide di numerare, inventa il contare e decide quanto e cosa valgano dei simboli. Come se si fossero seduti e avesse inventato una lingua a tavolino ((Conosci l'esperanto?)): un elenco di parole, suoni e significati. Eppure, quasi per magia, a distanza anche di migliaia di anni continuiamo a scoprire che questo muto elenco di segni ha in serbo sorprese, concatenazioni e legami che ci lasciano basiti, come se quei significati che abbiamo appioppato a suoni e simboli abbiano acquisito una propria essenza, o come se in fondo non avessimo fatto altro che rivelare qualcosa che già esisteva, ma che aveva solo bisogno di essere scoperto. Invenzione o scoperta?

Questo è il fascino della matematica per me, uno dei tanti. Ma torniamo in carreggiata!

I numeri poligonali

Tra le infinite proprietà dei numeri, partiamo da un fenomeno simpatico e semplice, che si presta facilmente ad una rappresentazione grafica e quindi è più facile da capire: i numeri poligonali.

Devi sapere amico Billy (oggi sono particolarmente magnanimo, ma ora zitto altrimenti spezzo il collo alla gallina della nonna) che tanto tempo fa, quando il tempo non ti rincorreva con un coltello insanguinato e le persone pensavano invece di lamentarsi, in Grecia alcuni matematici (o sarebbe meglio dire alcune persone alle quali piaceva interessarsi delle cose) rappresentando i numeri con un numero (il gioco di parole è dovuto) uguale di oggetti (ad esempio sassolini) scoprirono che era possibile formare delle precise figure geometriche (ma quante parentesi ho usato?).

L'esempio più famoso è quello del 10 della scuola pitagorica, che può essere rappresentato da un triangolo equilatero, come in figura.

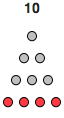
Incuriositi cercarono di trovare delle relazioni fisse che potessero generare questi particolari numeri, arrivando così a catalogare i numeri poligonali.

Numeri triangolari

Il pitagorico 10 è  proprio un esempio di numero triangolare, ovvero una quantità rappresentabile come un triangolo rettangolo isoscele o come un triangolo equilatero. L'ennesimo numero triangolare si può ottenere attraverso la sommatoria dei primi n numeri.

Per andare molto sul concreto, se vogliamo arrivare al nono numero triangolare basterà calcolare la sommatoria dei primi 9 termini, ovvero:

0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

Come abbiamo già anticipato, questi numeri sono rappresentabili come triangoli. In particolare, se pensiamo di disporli come triangoli rettangoli isosceli, accostandogli vicino un triangolo uguale (congruente, come ci insegnavano alle elementari) otteniamo un rettangolo che ha un numero di righe pari al numero che era originariamente rappresentato dal triangolo, mentre il numero maggiorar di uno per le colonne. Wikipedia vi può aiutare a visionare il tutto:

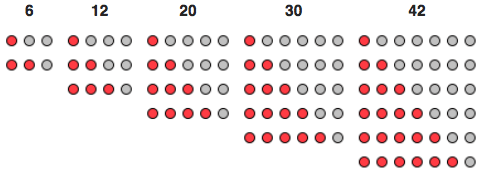
Grazie a questo piccolo trucchetto e richiamando stralci di geometria elementare (l'area di un triangolo è la metà dell'area del rettangolo formato "duplicando il triangolo", proprio come abbiamo fatto noi) otteniamo così la formula per ottenere l'ennesimo numero triangolare, abbiamo ovvero ottenuto una delle tante formule di Gauss:

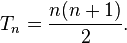
Gauss e la somma dei numeri da 1 a 100

Riporto scorrendo lo scritto di Alessandra Fiocca:

Uno dei più famosi aneddoti della matematica riguarda Karl Friederich Gauss bambino. Si racconta che Gauss fu educato in una squallida scuola diretta da un tale, chiamato Büttner, il quale aveva l’abitudine di assegnare alla classe lunghi problemi di aritmetica, che lui poteva facilmente risolvere formule conosciute, con l’obiettivo di tenere occupati gli scolari. Un giorno l’insegnante diede agli alunni il compito di calcolare la somma dei primi 100 numeri naturali, sicuro che questo lavoro li avrebbe impegnati per un po’ di tempo. Il piccolo Gauss, poco dopo che l’insegnante ebbe terminato la dettatura, si avvicinò alla cattedra e, posando il foglio su di essa, esclamò “Ligget se” (Ecco qui). Poi, ritornò a sedere e rimase per più di un’ora con le braccia conserte attendendo che i suoi compagni terminassero il lavoro. Nel frattempo Büttner osservava sarcasticamente questo bambino che riteneva fosse solamente un altro spaccone. Quando, però, andò a controllare il lavoro svolto dal piccolo allievo vi trovò solamente un numero, 5050, la risposta corretta al quesito posto. Possiamo solo immaginare lo stupore dell’insegnante di fronte a questa risposta, sapendo benissimo che il piccolo non poteva conoscere la formula n(n+1)/2 e che certamente, dato il tempo di consegna, non poteva aver calcolato esplicitamente tutta la somma. Quale procedimento utilizzò allora il piccolo genio per trovare il risultato?

Esattamente quello che ti ho appena mostrato: disponendo i primi n numeri che vogliamo calcolare come delle pile di mattoncini, la somma di questi può essere facilmente calcolata notando che, duplicando il "triangolo" che si viene a formare ottengo un rettangolo di area (n+1)*n. Dato che noi siamo interessati alla sua metà (ovvero alla sola area del "triangolo"), facciamo un bel "fratto due".

Bimbi prodigio.

Bravo Billy! Ora che ti sei elevato all'intelligenza di un castoro celebro-leso chiudi gli occhi e ascolta (poi riaprili e leggi, a meno che tu non sia Clark Kent): la somma di due numeri triangolari successivi genera sempre un quadrato perfetto. Quindi, la somma di due triangolari successivi genera un numero quadrato (un numero intero che può essere espresso come il quadrato di un altro numero intero).

Ma non è finita: la somma dei primi n numeri triangolari genera un numero tetraedrico! ((La congettura di Sir Jonathan Frederick Pollock asserisce che ogni numero naturale può essere rappresentato come la somma al massimo di cinque numeri tetraedrici. La congettura non è stata completamente dimostrata perché molto difficile, ma viene largamente accettata come vera.))

Il triangolo di Tartaglia

Ovviamente, non è finita qui. Non è mai finita qui quando si parla di scienze. Alzi la mano chi non conosce il triangolo di Tartaglia?

Bhe, è abbastanza famoso.

E invece quanti di voi sanno che Tartaglia era un soprannome affibbiato al matematico a seguito di un brutto incidenze che gli causò un' accentuata balbuzie?

Bitch please.

However, il ma-ma-ma-matematico (senza offesa per chi ne soffre, perdonatemi ma era d'obbligo) costruì quindi questo straordinario marchingegno numerico, ovvero un triangolo in cui ogni numero, tranne il numero generatore al vertice del triangolo, è la somma dei due numeri sovrastanti. Ai bordi si trova sempre l'1, poiché i due numeri sovrastanti sono, in questo caso, da una parte 1 e dall'altra nessun numero, cioè zero (read here).

Non mi dilungherò molto sulle migliaia di proprietà di questo triangolo (almeno non oggi, /occhiolino ammiccante che lascia intendere qualcosa/) perché sono interessato a ben altro. Disponendo il triangolo di tartaglia alla maniera di Pascal, che lo rese famoso, notiamo che la terza colonna a partire da sinistra è formata dai numeri triangolari!

Ci sono altre n cose che potrei dirti, ma fa troppo caldo ed è giusto che io mi vada a fare il bagno mentre tu vieni assorbito nei meandri del web cercando, ad esempio numero pentatopico o numero pentagonale.

Per rimanere nel nostro bellissimo blog invece, potreste leggere qualcosa sulla struttura fine o sui numeri più grandi immaginati.