Diciamocelo Billy, parliamo a tu per tu: trascurando la doccia, le sedute sul wc sono il momento più ispirante delle tue giornate. Stai lì, con lo sguardo perso a fissare le mattonelle di fronte a te e con bocca semi aperta ti lasci trasportare da flussi di coscienza che fanno nascere riflessioni profonde.

A questo punto ti starai già chiedendo allora per quale motivo un articolo scientifico debba iniziare con un Billy seduto sulla tazza del water. Se ricordi abbiamo già parlato della chimica e della fisica delle puzzette, per cui, almeno per questa volta, tralasceremo tutte le considerazioni sulla fisiologica natura dell’uomo come essere defecatore.

Oggi si parla di gabinetti e non solo! Scaveremo insieme nell’intrinseca natura degli scarichi per dare risposta ad una domanda che alcuni si pongono e a cui non trovano risposta: osservando un generico scarico, che sia del WC, del lavello o della vasca da bagno, esiste una direzione predefinita nella rotazione dei vortici?

Se sei un appassionato dei Simpson  ti ricorderai sicuramente l’episodio “Bart contro  L’Australia ” ((puntata dei Simpson in streaming)) , in cui per sconfessare la rivelazione di Lisa secondo cui il verso di rotazione dei vortici negli scarichi dipenda dall’emisfero in cui ci si trova, Bart chiama fino in Australia, dando vita così ad una fantastica puntata.

Lisa ha davvero ragione?

Partiamo dagli inizi.  (Se non vuoi leggere il pippone fisico-matematico salta fino a Ж, la tua conoscenza non risentirà di questa mancanza)

Come per la meccanica classica esiste la legge di Newton, per la meccanica quantistica l’equazione di Schrödinger, anche per i liquidi, o in generale per i fluidi esiste un’equazione che ne descrive il comportamento: l’equazione di Navier- Stokes.

Il primo, Claude Louis Navier, un ingegnere. Il secondo, George Gabriel Stokes, un matematico.
Come puoi ben immaginare dall’unione di queste due figure semi-mitologiche non può che nascere qualcosa di profondamente diabolico. L’equazione di Navier- Stokes è, infatti, uno dei sei problemi del millennio ancora irrisolti della matematica.

Per essere più precisi, però, sarebbe più corretto parlare di un sistema di equazioni, ben quattro, di tipo differenziale alle derivate parziali. ((derivazione completa equazioni di navier –stokes)) Te le faccio vedere:

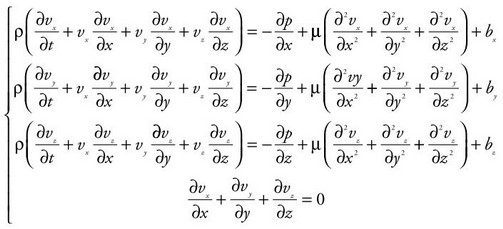
 Le prime possono essere raccolte sotto forma di un’unica equazione di tipo vettoriale e utilizzando i diversi operatori differenziali, la cui definizione è inutile per arrivare a comprendere l’articolo, le equazioni diventano:

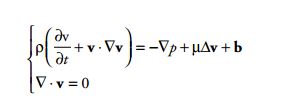
Ti starà chiedendo perché le ho riportate se non servono direttamente per capire l’articolo:

• Devi effettivamente renderti conto che non si capisce una cippa e non solo per te che non hai mai magari affrontato esami di analisi: esistono infatti matematici che stanno sbattendo la testa da decenni sperando di giungere alla soluzione, cosi da vincere il milioncino di dollari offerto dal premio dell’istituto matematico Clay.
• Ti teniamo compagnia ormai da molto tempo è giusto che ti renda conto che la vita non è così facile come ti lasciamo lasciar credere in ogni articolo!

Ormai sei diventato grande, puoi addirittura entrar a far parte de “la Palestra” e i grandi guardano l’equazioni differenziali con sprezzo del pericolo e voglia di fare!

Cerco di farti capire un po’ il tutto.

Ciò che i due scienziati hanno fatto è stato costituire un’uguaglianza tra equazioni dette di bilancio. Un’equazione di bilancio è una legge che descrive l’andamento di una determinata quantità all’interno di un volume di riferimento. Letteralmente può essere scritta come:

(quantità entrante)+ (quantità uscente)+ (produzione) =(accumulo)

Le prime tre equazioni, nel sistema precedente,  rappresentano un’uguaglianza tra l’equazione di conservazione della massa a quella della quantità di moto. L’ultima equazione è una forte semplificazione del problema perché indica che il fluido in considerazione ha una densità costante.

Pensa Billy che l’equazione così descritta considera la materia come una quantità continua, ignorando la granularità dovuta alla presenza delle molecole, trascura inoltre i contributi elettromagnetici e quelli dovuti alla presenza di reazioni all’interno del fluido. Già cosi è impossibile, cosa diventerebbe se si dovessero considerare tutti i contributi?

Ж

Avendo capito che non siamo capaci di utilizzare una modellizzazione matematica per descrivere il senso di rotazione dei vortici dobbiamo ricorrere al metodo sperimentale. Svolgeremo innumerevoli esprimenti per confermare che sopra l’equatore, nell’emisfero boreale, i vortici scorrono in senso antiorario, mentre al di sotto, in quello australe, in senso orario.

Hai un permesso di cinque minuti per aprire il maggior numero di rubinetti per vedere in che senso è la rotazione

Fatto? Bene (cit. Giovanni Mucciaccia)

Probabilmente sarai giunto a risultati inconsistenti. Alcuni scarichi avranno creato vortici che girano in senso orario, altri in senso antiorario. Possiamo per cui concludere che questa storia del senso di rotazione sia una grande baggianata? Not so fast, Billy.

Da bravi appassionati di scienza pensiamo cosa sia potuto andare storto e modellizziamo il fenomeno fisico. Ciò che dovrebbe indurre una rotazione è la cosiddetta forza di Coriolis.

FORZA DI CORIOLIS

È una forza di tipo apparente, quel genere di forze che si manifestano quando un osservatore inerziale è posto in un sistema di riferimento non inerziale, cioè accelerato. Per ripetere per la miliardesima volta lo stesso esempio, una forza di tipo apparente è quella che risente un corpo su un mezzo durante una frenata.

In questo caso la forza descritta è quella che risentirà un corpo quando esso sarà in moto rispetto un sistema di riferimento rotante. L’azione della forza sarà visualizzabile da un osservatore esterno all’oggetto in moto nel sistema in rotazione.

Nel primo disco si osserva come la pallina vede il proprio moto (osservatore solidale al sistema inerziale). Nel secondo ci sei tu Billy, che guardi dall’esterno ciò che avviene (osservatore esterno). In pratica la forza di Coriolis agisce curvando la traiettoria di un corpo che nel suo sistema di riferimento si sta muovendo in maniera rettilinea.

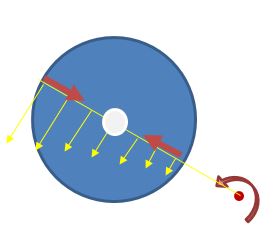
Il sistema rotante nel nostro caso è la terra in rotazione attorno al proprio asse, mentre la particella in moto è quella che dagli estremi del lavandino si muove fino allo scarico. Ogni molecola di acqua sarà soggetta al momento dovuto alla rotazione terrestre più un ulteriore forza che la spinge verso lo scarico.  La figura rappresenta come dovrebbe apparire il sistema delle forze. Considerando il puntino rosso come l’asse attorno cui ruota la terra e il cerchio bianco come lo scarico. Nota bene la figura rappresenta una forte semplificazione poiché considera il piano su cui è posto lo scarico trasversale all’asse di rotazione.

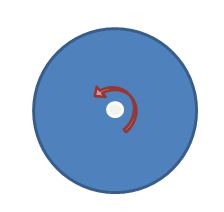
Combinando le due forze ciò che viene fuori è un moto rotatorio attorno lo scarico. Naturalmente il verso di rotazione della terra varia in base all’emisfero considerato: senso antiorario per l’emisfero boreale e senso orario in quello australe. Questo dovrebbe ripercuotersi sul sistema e quindi visualizzarsi nella vorticosità degli scarichi.

Ancora non abbiamo risolto l’arcano! Proviamo a buttare giù qualche conto!

Attenzione! I calcoli contengono delle forti semplificazioni che non nuocciono alla salute (se vuoi puoi provare a ripeterli a casa)!

La forza  di Coriolis in forma estesa può essere scritta come:

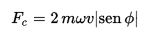
• ω è la velocità angolare della terra pari ad un giro cioè 360° in un giorno cioè 24 h, che convertito in radianti al secondo diventa pari a 7.27 10^-5 .
• v è la velocità che una generica molecola d’acqua risente nel mentre in cui viene risucchiata verso lo scarico. Se si considera ad esempio un lavello circolare di raggio 30 cm, con lo scarico posto nel centro. Ipotizzando che una molecola dall’estremo del lavello impieghi 10 secondi per raggiungere lo scarico, la velocità sarà 0.03 m/s.
• m è la massa della particella che potrebbe essere benissimo una molecola di acqua con una massa di 2,988 10^-26 kg.
• Infine ϕ è l’angolo formato tra ω e v, che nel nostro caso è pari a 90°, per cui il seno sarà pari ad 1

Sostituendo tutti i dati, la forza di Coriolis che risente una singola molecola di acqua è per cui:

Fc=1.3*10^-31 N

A questo punto è necessario considerare tutti gli altri fattori che potrebbero influire sul moto della molecola. Trascurando gli effetti geometrici del lavandino, ipotizzando che la sua forma sia perfettamente circolare, si passa invece a considerare la forza impressa alle molecole, dovuta alla pressione della rete idrica nelle tubature.

Ipotizzando che la pressione sia pari ad 1 atmosfera e che il diametro del rubinetto sia pari a 2 cm la forza con cui il flusso di acqua fuoriesce:

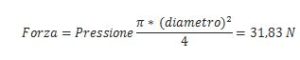
Inoltre riconsiderando lo stesso diametro del rubinetto e semplificando la forma della molecola di acqua come circolare di diametro pari a 10^-10 m, per ogni istante le molecole che attraversano il rubinetto sono circa 10¹⁶. Per cui ogni molecola risente di una forza:

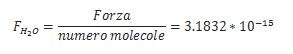
Tieniti forte Billy, siamo forse giunti ad una conclusione. Confronta quest’ultimo risultato con quello della forza di Coriolis: la forza della pressione è ben 16 ordini di grandezza più grande di quella di Coriolis.

Cosa si può concludere?

Tutte le forze rispetto a quella di Coriolis sono enormemente maggiori, rendendo l’effetto della vorticosità, dipendente dalla rotazione terrestre, non direttamente visualizzabile.

I fantastici vortici che comunque si formano negli scarichi sono dovuti a forze esterne e quindi sono comunque presenti.

Ma non ti abbattere. Esiste effettivamente un modo per visualizzare l’effetto Coriolis. L’idea è di costituire un sistema isolato, su cui non agisca alcun tipo di forza. Ad esempio sarebbe possibile riempire una vasca ed attendere che si stabilizzi, e solo successivamente aprire lo scarico.

Un po’ come hanno fatto questi due:

 Nihil sub sole novum