E' nato prima l'uovo o la gallina? Sulle risposte inattaccabili

Tempo fa ero in California (BR), intento a cercare misteriose regolarità dell'universo e mentre incrociavo dati di vario genere, inciampai in una potenziale scoperta che avrebbe potuto cambiare il destino della ricerca scientifica.

Trovai, infatti, che più le università impiegavano denaro in scienza e tecnologia, finanziando la ricerca, e più aumentava il numero di gente che s'ammazzava impiccandosi. E non è tutto: non appena il finanziamento agli enti di ricerca calava, calavano i suicidi per impiccagione, per poi aumentare solo se aumentava daccapo il denaro speso in R&S. Poteva essere solo una macabra coincidenza? L'implacabile sete di dettagli doveva essere colmata: detti in pasto il tutto ad un computer e ne rimasi agghiacciato. Fu così che decisi di pubblicare i risultati e qui di seguito riporto il grafico che mostra inconfutabilmente quanto sopra.

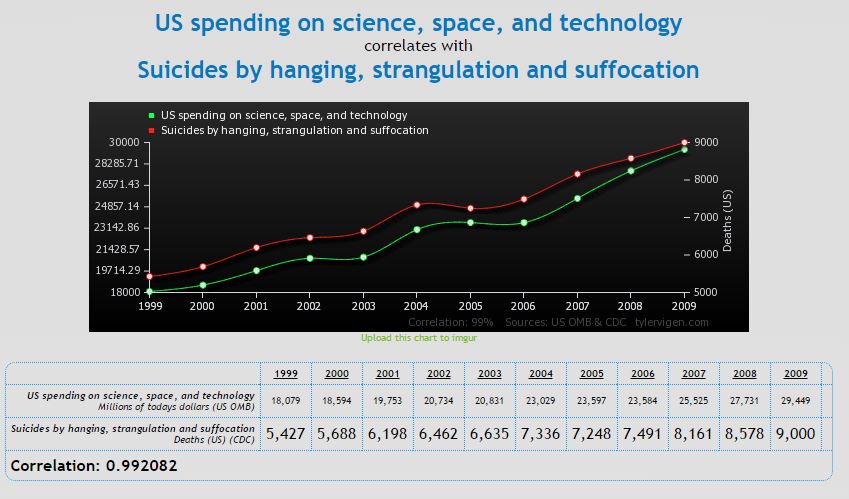
Ebbene, come chiunque di voi può facilmente provare con un software statistico, vi è correlazione pressoché unitaria tra le due cose. Era ormai notte fonda e ne conclusi che si doveva drasticamente ridurre la spesa pubblica dedicata alla ricerca scientifica in modo da interrompere il terribile flusso di suicidi per impiccagione: la mia era una risposta inattaccabile.

All'indomani, impacchettai i dati con cura e li inviai ad una importante rivista scientifica, presso la quale avevo un contatto. Non ebbi mai risposta, ma il contatto, che abitava poco distante da casa mia,  da quel giorno smise di salutarmi: non voglio però essere malizioso; credo quest'ultima sia solo una coincidenza.

CORRELAZIONE NON SIGNIFICA CAUSALITA'

Questa inflazionata ma sacrosanta verità demolisce la fantasia alla quale si deve la storiella sopra. Negli ultimi tempi, soprattutto sul web, citare questa frase si sta rivelando una moda! L'avete mai sentita? Se la risposta è no, riserverò a voi un breve inciso, per poi passare al cuore del discorso: le uova e le galline.

E' paradossale il fatto che sovvenzionare la ricerca scientifica causi un incremento di suicidi per impiccagione, sebbene sia vera la correlazione unitaria che lega le due cose. Mi spiego meglio. Come è evidente dal grafico, in cui la curva in verde mostra la spesa per la ricerca scientifica e quella rossa il numero di suicidi, i due fenomeni sono strettamente (e positivamente) correlati: quando una curva aumenta, l'altra aumenta; quando l'una diminuisce, l'altra la segue. E' possibile misurare questa tendenza di alcuni eventi a "variare all'unisono" con il concetto di correlazione tra gli stessi: per ciò che è qui di interesse basti sapere che più ci si avvicina ad 1 e più i fenomeni saranno correlati ed è per questo che la correlazione della favola bella di cui sopra, pari a 0.99, è incredibile. Vi stupireste di quanti fenomeni apparentemente senza legami, sono strettamente correlati. Qualche esempio?

• il numero di persone che affogano in piscina e il numero di film in cui compare Nicolas Cage;
• il consumo di formaggio negli Stati Uniti e le persone che muoiono aggrovigliate tra le lenzuola;
• la produzione di miele e gli arresti di giovanissimi per possesso di erba.

Qual è il punto? La correlazione non implica la causalità: che un evento sia correlato ad un altro, finanche in maniera molto marcata, non vuol dire affatto ne sia la causa. E' bene tenerlo a mente, nel periodo in cui sedicenti esperti propongono rapporti di causa-effetto più o meno stravaganti (penso ad autismo e vaccini, wi-fi e tumori, immigrati e declino della società occidentale).

Detto ciò devo ammettere che in molti han parlato della differenza tra correlazione e causalità (io stesso qualche tempo fa, sul mio profilo Fb personale!) e qualcosa di nuovo bisogna pure aggiungerla.

E' NATO PRIMA L'UOVO O LA GALLINA?

Ho detto cosa la causalità non è - e cioè correlazione - ma non ho detto cosa in realtà essa sia. Leggevo che un assunto fondamentale del diritto è che ogni evento abbia una causa a monte, alla quale fare appello per emettere un giudizio. Dal punto di vista filosofico la cosa si complica, ma per in linea del tutto generale qui dirò che è causa di A ogni condizione dell'evento A, senza il verificarsi della quale A non si sarebbe prodotto. Dunque la gallina è conditio sine qua non perché ci sia un uovo, in quanto senza di essa questi non si sarebbe di certo generato dal nulla. D'altra parte non c'è gallina se non c'è uovo. E dunque chi la spunta?  Per non disseccare il tutto nella aberrante possibilità di regressus in infinitum, un recedere all'infinito nella ricerca della causa ultima dell'evento, ragioniamo come segue.

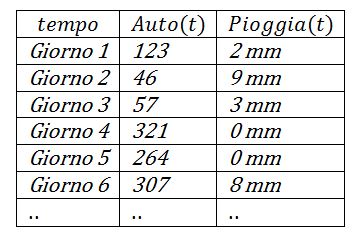
Date due serie temporali di dati, da ora x(t) e y(t),  che esprimono l'evoluzione di un fenomeno stocastico nel tempo, ci si può chiedere se e in che modo l'una possa influenzare (in un certo senso causare) l'altra: è proprio la nostra domanda. Un esempio ? Eccovi due fenomeni stocastici che evolvono nel tempo: il numero di auto che transitano sul ponte ogni giorno ed i millimetri di pioggia che vi cadono quotidianamente.

Sotto opportune condizioni possiamo esprimere la dinamica di un determinato processo del tempo come una funzione dei suoi valori passati e di un errore u , sul quale non mi dilungherò (anche se servirebbe!).

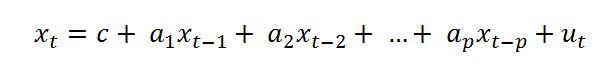
Dunque l'informazione sul valore futuro del fenomeno è data dai valori passati. Se ora introduciamo un secondo fenomeno nel calderone, ad esempio i mm di pioggia, che influenza ha questo sul fenomeno iniziale considerato?  Ne è causa? E' correlato? Non lo è? Nello specifico ricordo che il nostro dubbio è se in qualche modo ne è la causa.

Per ricambiare chi vi scrive dello sforzo di non usare matematica (che qui renderebbe tutto più semplice, a patto di saperla leggere!), chi legge deve prestarmi un poco d'attenzione:  In sostanza ci chiediamo se, nel prevedere valori futuri di un generico fenomeno y, il fenomeno x dia ulteriori informazioni rispetto ai soli valori passati di y.  Al netto di stiamo chiedendo se x sia "Granger - causa" di y. E' così che si dice in gergo.

Dopo questa (iper -semplificata) premessa teorica entriamo nell'aia. Userò due serie storiche dei nostri fenomeni da studiare:  galline(t)  e uova(t), che vanno pensate come quelle dell'esempio precedente. Queste raccolgono i dati annuali sul numero di galline (milioni) e di uova (milioni di dozzine) dal 1930 al 1983. Graficando l'andamento nel tempo dei due fenomeni:

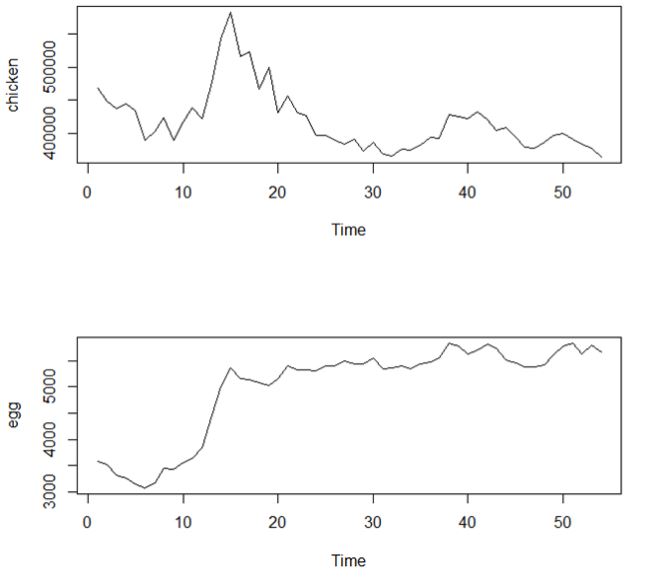
non risulta immediata alcuna conclusione. E' necessario un po' di lavoro sporco! Avvalendosi dell'ambiente statistico R, un software open source trai più usati per cose come statistica e machine learning, ed operando opportuni passaggi per preparare i dati alla analisi, si va a testare se:

uova(t)    causa    gallina (t) ;

oppure

gallina(t)    causa    uova(t);

che è una traduzione statistica della domanda di fondo: " viene prima l'uovo o la gallina?". Badando bene che ogni qual volta si è parlato in termini di "x causa y", si è inteso che x causa y nel senso di Granger, si può giungere alla conclusione del test statistico:

1. Tesi "viene prima l'uovo e poi la gallina": si può rifiutare l'ipotesi che l'uovo non precede la gallina.
2. Tesi "viene prima la gallina e poi l'uovo": non ci sono evidenze per rifiutare l'ipotesi che la gallina non precede l'uovo.

Se ne conclude, trasformando il risultato "1." in forma positiva, che l'uovo viene prima della gallina, il che è una risposta inattaccabile. Per chi avesse dimestichezza con gli strumenti utilizzati, i risultati del paper originale, assieme ai dovuti chiarimenti su come trattare simili peripezie, sono raccolti in tabella.

UN'AMARA CONCLUSIONE

Quelli che ho proposto sono giochi (e come tali van presi!) atti a consegnare a chi legge una questione quanto mai attuale, con cui mi avvio a concludere.

Viviamo il tempo di Big Data, del web, dei social, in cui la potente (eppure limitata) macchina scientifica produce sapere  spesso disallineato con ciò che viene poi divulgato su giornali e riviste dedicate al grande pubblico. Da un lato vi sono i limiti concettuali delle scienze matematiche e statistiche che vengono spremute fino all'osso, talvolta con risultati disastrosi in ambiti assai gravidi di conseguenze (economia, scienze sociali, medicina). E' così che, con strumenti rigorosi, ma con il naso tappato e qualche assunzione di troppo, inferisco su un dilemma millenario come l'uovo e la gallina, trovando una risposta inattaccabile, che senza didascalie avrebbe del tutto convinto i meno avvezzi alla pratica del dubbio. Sul fronte opposto, la mistificazione dei risultati da parte di chi fa da tramite tra mondo accademico e grande pubblico, affiancata dal pensiero veloce, da tweet, produce assiomi "ad alta digeribilità" che di vero hanno ben poco. Basta un attimo che le risorse dedicate alla ricerca (a patto le si trovino!) siano motivo di suicidi per impiccagione.

Prolifera, così, la pseudoscienza , foriero di scazzottate (digitali) mai intraprese da ragazzini, tra chi sostiene l'una e chi l'altra verità, sebbene, in molti casi, non ve ne sia che una sola, di verità. Talvolta la super-cazzola (in linguaggio tecnico) di cui la pseudoscienza si nutre arriva perfino in Parlamento. Altre volte è soltanto motivo di polarizzazione tra comuni cittadini viziati dalle strane dinamiche del web. Tra teorie del complotto, inesattezze, o più semplicemente falsità, si spande tra i bar, s'insidia sui social, prolifera, e ogni tanto qualche pargolo non vaccinato ne paga addirittura le conseguenze con la vita. Complice il pregiudizio di conferma - per il quale tendiamo a favorire le informazioni che confermano le nostre tesi, scartando le altre - il fenomeno della disinformazione pare inarrestabile: impazzano così le infuocate diatribe su chi sia capostipite del nuovo ordine mondiale, o sulla nuova dieta dell'estate a base di monossido di diidrogeno e lampascioni. Dovremo farcene una ragione.

La risposta inattaccabile, che è così perché lo dico io, è un lupo sempre in agguato, che talvolta grafici e complicate equazioni possono mascherare a dovere. E' un effetto collaterale della libera circolazione dell'informazione, che nei cablaggi corre più forte del denaro e di noi uomini , il cui unico antidoto è la pratica del dubbio anche e soprattutto rispetto alle proprie convinzioni.