Il paradosso dei due condensatori

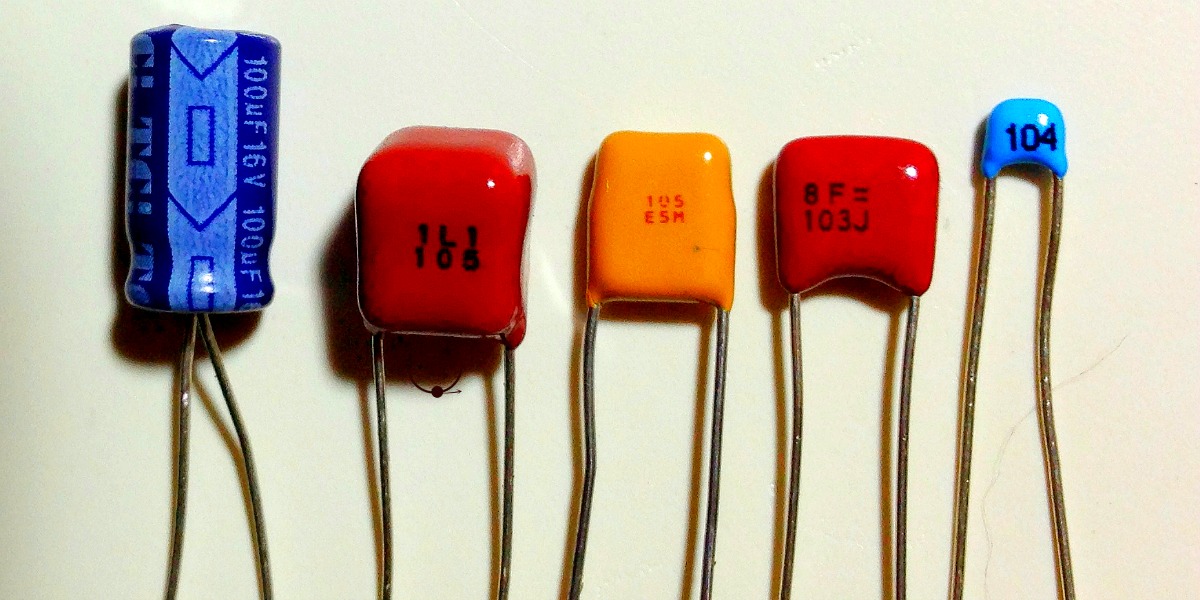
Ciao Billy, sono nuovo di qui, quindi abbi pazienza con me. Oggi è un giorno particolare, perché con questa storiella inauguro la nuova sezione “Paradossi”.

I paradossi sono divertenti sai, prima ti sembra di essere davanti a qualcosa di impossibile, tutto quello che sai riguardo quell'argomento ti si rivolta contro, i tuoi sforzi nell'applicare leggi così ben collaudate sono buchi nell'acqua. Perché i paradossi sono spesso casi limite, che i più pragmatici potrebbero definire "inutili perdite di tempo", le cui condizioni non possono essere riprodotte nella realtà. Ma è come pensare che guardare Harry Potter sia stupido perché "tanto chi invocherà mai un Avada Kedavra?": lo scopo è diverso. I paradossi sono pane per la fantasia, una Palestra dell'immaginazione.

Quindi, cambiati ed andiamo ad allenarci.

Prima di iniziare ti spiego brevemente cos’è un condensatore.

Un condensatore è uno strumento che serve a immagazzinare energia depositando in esso delle cariche elettriche. Una volta “caricato”, un condensatore possiede un’energia proporzionale al quadrato della carica che contiene. Ogni condensatore è caratterizzato da una capacità C che indica, in parole così tanto povere che non hanno neanche un dizionario dove dormire, “quanta carica” può tenere. Giusto perché tu lo sappia (e anche perché tra poco ci servirà) l'energia immagazzinata è:

$$E_{tot}=\frac{Q_{0}^{2}}{2C}=E_{0}s=3$$

Detto ciò iniziamo:

Tipico esempio di condensatore triste ed isolato.

Allora Billy prendi un condensatore isolato, cioè che si trova da qualche parte da solo e lontano da qualsiasi cosa che possa interagire con lui (sì, è una storia commovente), contenente una carica $$Q_{0}s=3$$ e quindi con potenziale $$V=\frac{Q}{C}s=3$$ ai capi delle due armature. L’energia immagazzinata da questo condensatore è $$E_{0}=\frac{Q_{0}^{2}}{2C}s=3$$.

Tieniti forte Billy: colpo di scena. Ad un tratto ecco spuntarne uno identico, ma completamente scarico come in figura:

Cosa faranno i due condensatori? Faranno all'ammore? Si andranno ad abbufare ad un all you can eat sushi? Calcetto in amicizia?

Niente di tutto ciò. I condensatori sono dei tipi seri, dai saldi principi. In particolare ce ne sono due che sono costretti a rispettare: devono conservare la carica e l'energia.

E non perché siano delle parsimoniose formiche, piuttosto perché non è possibile creare o distruggere energia o carica. Almeno fino a prova contraria.

Succede quindi che una volta collegati i due condensatori, secondo quanto ci viene detto dall'elettrostatica, questi devono portarsi allo stesso potenziale: essendo la capacità identica, è ragionevole che ciascuno si prenda metà della carica iniziale.

E l'energia? Beh Billy, questa volta ti tocca leggere due formule, almeno capisci che faccio sul serio:

$$E_{tot}=E_{C_{1}}+E_{C_{2}}=\left(\frac{Q_{0}}{2}\right)^{2}\frac{1}{2C}+\left(\frac{Q_{0}}{2}\right)^{2}\frac{1}{2C}$$

Beh tutto chiaro fin qui no? Bene continuiamo allora!

$$E_{tot}=\frac{Q_{0}^{2}}{8C}+\frac{Q_{0}^{2}}{8C}=\frac{Q_{0}^{2}}{4C}=\frac{E_{0}}{2}$$

Ecco Billy, vedi ora c'è qualcosa che non va...Conserviamo la carica, e scopriamo che l'energia totale del sistema si è dimezzata. Se ti va, puoi provare a imporre la conservazione dell'energia in partenza, e scoprirai che a non conservarsi più è la carica, che diventa ben $$\sqrt{2} s=3$$ volte più grande! (altrimenti fidati di me)

Chiariamo quindi qualche aspetto cavilloso della vicenda, prima che ti ci possa aggrappare sventolando l'indice come un predicatore americano: i fili e i condensatori sono ideali, non presentano quindi alcuna resistenza al passaggio di corrente (se vuoi fare il pignolo, considera il tutto fatto di superconduttori in un #superfreezerdellamammaadelioliquido).

Questo è il punto che distingue un problema molto semplice da un paradosso: l’energia non può essere dissipata per effetto Joule!

Quindi, mio caro nuovo amico, dov'è finita l'energia? Applichiamo la conservazione della carica e trasgrediamo la conservazione dell'energia. E, conti alla mano, procedendo in modo contrario conserveremmo l'energia ma non la carica.

C'è qualcosa che evidentemente non quadra.

Che dire, l’elettrodinamica non è proprio l’argomento più intuitivo della fisica, ma possiamo fare una bellissima similitudine (che volendo può essere dimostrata) con una situazione di tutti i giorni (più o meno): consideriamo una molla.

Lo scopo della vita di un condensatore è quello di accumulare energia (attraverso il deposito di cariche) da rilasciare quando c’è bisogno; beh Billy è un po’ quello che fa anche una molla, non trovi?

Tu la schiacci finchè vuoi e intanto lei accumula energia, poi quando la lasci la restituisce (non l’accumula per mezzo di carica ma di qualcos’altro, ma il concetto è quello). Qui c’è il punto chiave del problema: a cosa/chi rilascia energia? Tu dirai “che domande, al corpo che è attaccato”. Bene, poniamoci nel caso in cui alla molla non sia attaccato nulla, nessun corpo da spostare. E ora? La risposta la conosciamo tutti: la molla oscilla da sola; ma un corpo senza massa come fa a oscillare?

La risposta è: la molla è anche la massa!

Beh Billy, se ci pensi la molla deve essere costruita con qualcosa, alluminio per esempio, che seppur leggero un po’ di peso ce l’ha! Quindi la molla oscilla da sola, usando l’energia accumulata per spostare “il materiale di cui è fatta”.

Giustamente ti starai chiedendo il perché di tutto questo discorso. Ti ho detto che la molla in meccanica si comporta esattamente come un condensatore in elettrodinamica. La domanda adesso è:

Ok, il condensatore accumula energia, ma come la trasmette? Cosa mette in movimento?

Mi dici la carica eh? Io ti dico di si, ma qui il discorso si fa delicato: la carica è il mezzo che il condensatore usa per portare l’energia ad un utente finale misterioso che in meccanica era la massa. Beh non abbiamo ancora risolto il problema in effetti: manca ancora qualcosa.

Ti faccio un’ultima domanda Billy: quando metti energia in uno strumento, dici che questo accumula energia potenziale, appunto perché è in grado di restituirla quando serve.

Ad un corpo in movimento che energia associ? L’energia cinetica!

Ci siamo ormai, abbiamo tutti i pezzi del puzzle, ma per chiarirti le idee continuo l’esempio della molla. Se la molla effettivamente non avesse massa propria (ed è chiaro che non esisterebbe, ma supponiamolo), oscillerebbe ad una velocità enorme, neanche misurabile, INFINITA!

La massa però, esistendo, carica la molla di un "peso" che rallenta l’oscillazione, permettendoti di misurarla; beh tale peso ha un nome e si chiama massa inerziale.

Vedi Billy, spiegarti bene il funzionamento di una massa inerziale necessità di un po' di numeri noiosi, per cui cerco di fartelo capire con una similitudine: sei al supermercato con papà, riempi tutto il carrello, inizi a correre spingendolo, e poi ti ci aggrappi. Mentre ti diverti a fare slalom tra le nonne non stai spingendo il carrello, ma è lui che sta usando l'energia che tu gli hai "fornito" prima per spostarti. Questo è quello che fa una massa inerziale. La molla mette in movimento la massa, poi arriva ad un punto detto "punto di equilibrio" in cui essa non la spinge più, a continuare il moto ci pensa la massa che "tirerà" la molla dalla parte opposta.

(Ok, scusa, torno ai condensatori)

Ormai abbiamo capito! Nel circuito dei due condensatori deve esistere l’equivalente di una massa inerziale, che rallenti inizialmente le cariche, che in caso contrario tenderebbero a muoversi a velocità infinita (?!?!?) verso il secondo condensatore, e che in seguito le porti tutte dal lui lasciando il primo condensatore completamente scarico.

Sarai felice di sapere che l’equivalente della massa esiste nel mondo elettrico: questo simpatico giocattolo si chiama induttore.

E ora caro Billy ti tocca beccarti una spiegazione dell'induttore. L'induttore è banalmente una o più spire fatte di un materiale conduttore. Prendi una penna, un filo e arrotolacelo attorno, bene, hai costruito il tuo primo induttore! Se non dovessi avere un filo a porta di mano te lo mostro: 

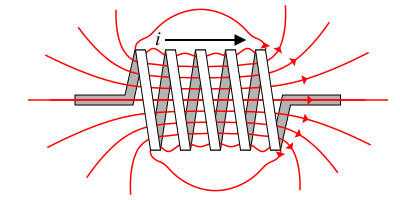
Cosa fa un induttore? Funziona come una massa inerziale, ma in un circuito: "rallenta" in un primo momento la corrente (quindi le cariche che si muovono) per poi poi rimetterle in moto. Un po' quello che fa il carrello con te quando smetti di spingerlo (e quindi di  accelerare) e ti ci aggrappi pronto a driftare nel reparto della verdura alla Fast and Furious!

Ora Billy ti faccio vedere qualche numero, non essenziale ma interessante, quindi se vuoi vai direttamente al punto wjdkbvjcvbkdf.

Una grandezza fondamentale quando si parla di correnti indotte (per scoprire bene cosa sono leggi qui ), è il flusso del campo magnetico, che puoi immaginare come "quanto campo magnetico" attraversa l'area della spira che hai costruito (in blu):

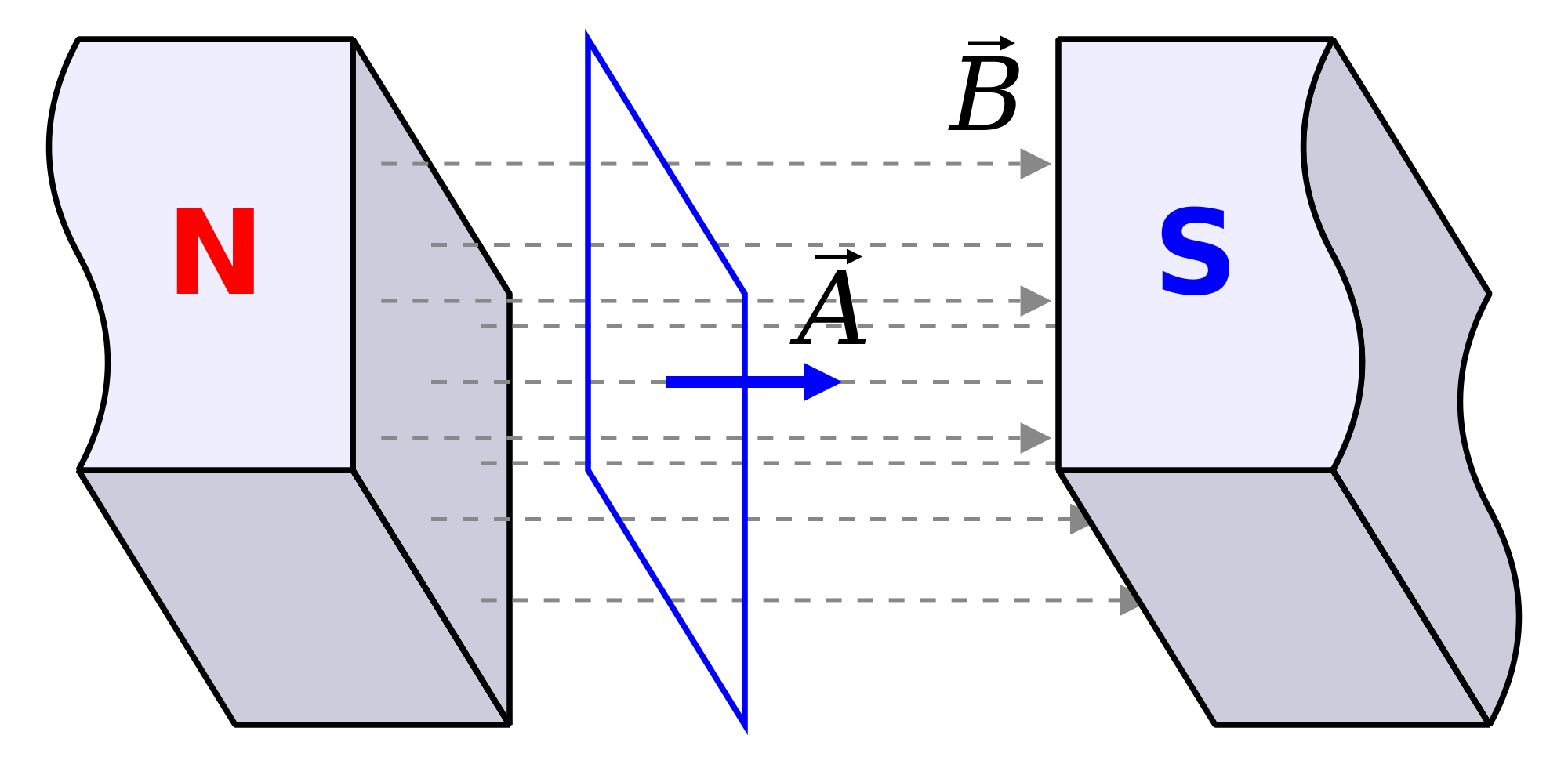
Si dimostra, anche se non te lo faccio vedere, che il flusso del campo magnetico $$\phi$$  attraverso una spira è direttamente proporzionale alla corrente I che scorre in essa; la costante di proporzionalità, detta induttanza L, identifica in modo univoco le proprietà del tuo induttore, e dipende unicamente dalla sua geometria. Se non ti sei ancora perso caro mio, mettiamo giù due formule:

$$\phi=LIs=3$$

Dalla legge di Lentz, sappiamo che la differenza di potenziale V ai capi dell'induttore è proporzionale alla variazione del flusso del campo magnetico all'interno della spira, ossia:

$$V=-\frac{\partial\phi}{\partial t}$$

Sostituendo la relazione dell'induttore nella legge di Lentz e derivando otteniamo:

$$V=-L\frac{\partial I}{\partial t}s=3$$

La presenza del segno meno indica che l'effetto dell'induttore è di opporsi alla variazione della corrente, "rallentandola" in una fase iniziale per poi ricondurla nel circuito.

wjdkbvjcvbkdf

Il suo lavoro è quindi quello di prendere tutta l’energia dal primo condensatore, un po’ alla volta, immagazzinarla, e poi nuovamente restituirla tutta al secondo condensatore, per poi ricominciare. Però Billy, dove viene messa l'energia che l'induttore accumula? Viene convertita in campo magnetico, il quale successivamente viene riassorbito, e la sua energia trasferita al secondo condensatore.

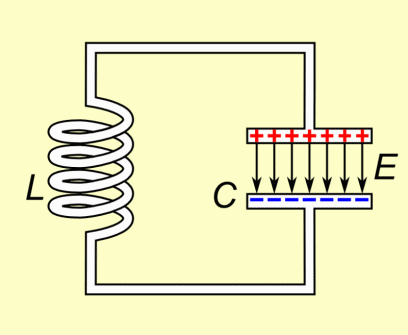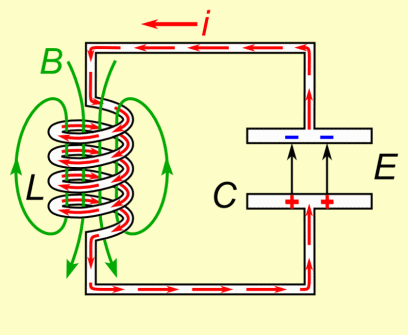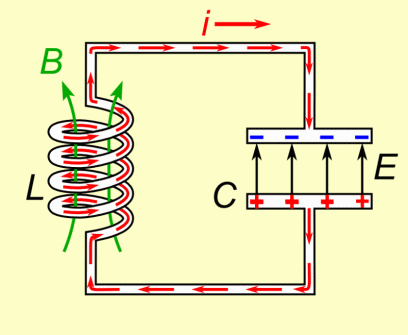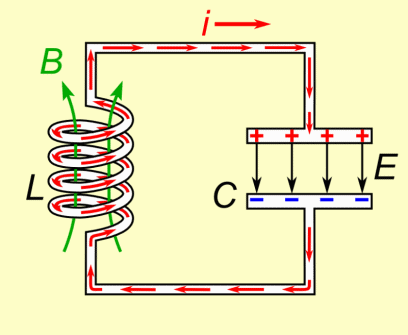
B è il campo magnetico, E quello elettrico nel condensatore, i la corrente.

Caro mio ora ti chiederai se sono impazzito, infatti il circuito con i due condensatori che ti ho mostrato non ha induttori! In realtà sì, collegando i due condensatori abbiamo di fatto creato un "circuito chiuso" che volendolo o meno è una spira e ogni spira è un induttore. 

Abbiamo quindi un circuito che oscilla tra due situazioni estreme: tutta la carica sul primo condensatore ed il secondo scarico, oppure tutta la carica sul secondo condensatore e il primo scarico. Questo grazie all'induttore che può essere visto come un agente del traffico per le cariche in moto che le guida in un certo percorso in modo temporalmente definito.

Così l’energia e la carica si conservano: i condensatori, come abbiamo detto prima, sono molto fedeli ai principi in cui credono. L'inghippo stava nell'accorgersi della presenza di un induttore "nascosto".

Approfondimento

In realtà succedono molte altre cose mentre le cariche si muovono: infatti si può dimostrare che se la geometria del sistema porta ad una valore di induttanza molto molto piccolo le cariche in moto non vengono "rallentate" a sufficienza, e quindi si trovano sottoposte ad una forte accelerazione e ciò ha una conseguenza molto forte: onde elettromagnetiche. Per darti una rapida idea, una carica accelerata genera un'onda elettromagnetica di potenza data dall'equazione di Larmor:

$$P=\frac{e^{2}a^{2}}{6\pi\varepsilon_{0}c^{3}}s=3$$

dove e è la carica dell'elettrone, a l'accelerazione delle cariche, c non te lo dico perché se sei arrivato a leggere fin qui devi saperlo. Una volta nota l'accelerazione, per calcolare quanta energia viene emessa sotto forma di onde elettromagnetiche basta integrare la potenza nell'intervallo temporale desiderato:

$$E=\int Pdt$$