Il teorema dei due carabinieri: anche in matematica vige la legge

Ciao Billy! Oggi ti spiegherò tutti i comportamenti da assumere, e da evitare, per rispettare al meglio le norme della legge italiana e garantire la convivenza civile all’interno della società.
E invece no, si parla di matematica!

~~Il lunedì migliore della mia vita~~

Abbiamo già trattato in precedenti articoli il Teorema della palla pelosa, ed ora è giunto il momento di approfondire un altro importante teorema denominato “Primo teorema del confronto”. Lo so Billy, lo so… immagino già cosa ti starai chiedendo: cosa c'entrano i carabinieri in tutto ciò? Non pretenderanno mica patente e libretto!

Eh no mio caro: dopo anni trascorsi a digerire silenziosamente crudeli e squallide battute (ammettilo Billy, almeno una volta nella vita anche tu hai raccontato una barzelletta sui carabinieri), questi esseri mitologici metà uomo e metà divisa approdano anche in campo matematico: oggi eccoli protagonisti di questo teorema, meglio conosciuto come “Il Teorema dei due Carabinieri”.

Alt! Mani in alto! (Aspettavo con ansia il giorno in cui avrei potuto dirlo)

Questa immagine sotto sotto ha la risposta: come vedi x₀ è un punto sulla retta dei numeri reali, ed è compreso in un intervallo molto molto piccolo, detto intorno $$I\left(x_0,\delta\right)$$, che va da$$x_0-\delta$$ a $$x_0+\delta$$, dove $$\delta$$ è un numero piccolo a piacere, ma ricorda: non è mai negativo!

Quand’è che x₀ si dice punto di accumulazione?

Quando all’interno dell’intorno esistono infiniti elementi di A. Eh si mio caro! È chiamato punto di accumulazione se anche in un intervallo molto piccolo, quasi impercettibile ai nostri occhi, sulla retta dei numeri reali puoi trovare infiniti valori.

Ecco un piccolo esempio per spiegare meglio il concetto: dell’insieme A fanno parte il punto 1 solo soletto e l’intervallo aperto fra 2 e 3.

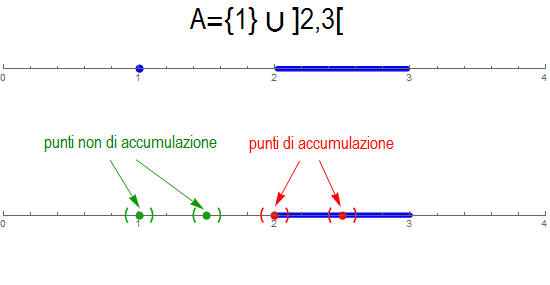
Se prendessi un intorno a piacere che va da 2 a 2.5 (in fig. di colore rosso) troverei all’interno di esso infiniti valori dell’insieme A. Se facessi la stessa cosa col punto 1, prendendo ad esempio un intervallo che va da 1 a 1.5 (in fig. di colore verde) non otterrei infiniti valori dell’insieme; in questo caso x0 è detto punto isolato.

Ci siamo quasi Billy! E se ora ti chiedessi…

Cosa si intende per limite finito di una funzione?

Non ti agitare, ti aiuto io: supponiamo di studiare una generica funzione y=f(x), la quale va da un sottoinsieme, denominato per comodità A (sperando che le altre lettere dell’alfabeto non si offendano), ad R, ovvero l’insieme dei numeri reali. Quando x tende a x₀ il valore della funzione f(x) tende ad l (numero finito appartenente ai reali) se:

“Per ogni intorno di l esiste un intorno di x0 tale che per ogni x appartenente all’Intorno di x0 (con x diverso da x0) si ha che f(x) appartiene all’Intorno di l”

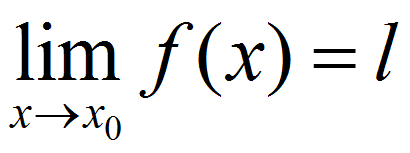
Questo, a grandi linee, è il concetto di limite finito per x che tende a x₀.

Se sei stato un Billy fedele ed hai letto fin qui nonostante conoscessi già l’argomento, ti sei appena guadagnato tutta la mia stima, dimmi tu se non è un premio speciale! Ma adesso arriva il bello...

Cosa afferma “Il Teorema dei due carabinieri”?

Siano h(x), f(x) e g(x) funzioni che vanno da A in R, x0 (in fig.1 c) un punto di accumulazione di A ed l un numero reale. Se esiste un intorno di c tale che per ogni x appartenente all’intorno di c (con x diverso da c), si ha che:

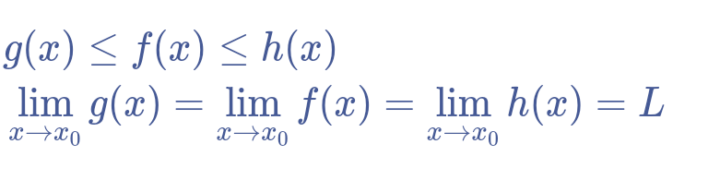
In parole spicciole spicciole: se le funzioni h(x) e g(x) tendono ad l per x che tende a x0 (in fig.1 c) allora anche f(x) è costretta ad avere limite l.

Io ancora non vedo traccia di carabinieri, e tu Billy? Il teorema è informalmente chiamato teorema dei due carabinieri per una semplice allegoria:

Le funzioni h(x) e g(x) personificano il ruolo dei carabinieri perché conducono in arresto un prigioniero, ovvero la funzione f(x). Questo delinquente, che è costretto a seguirli, tenderà sicuramente allo stesso punto dove tendono i carabinieri, pertanto avrà lo stesso limite.

La giustizia trionfa ancora una volta...ed anche la matematica! Alla prossima, Billy!